
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7 |
分析 (1)利用描点法可得图象;
(2)根据所给的数据,做出变量x,y的平均数,求出b,a,即可求线性回归方程;
(3)当自变量为10时,代入线性回归方程,求出维修费用,这是一个预报值.
解答 解:(1)散点图如图:
(2)$\overline{x}=4$.$\overline{y}=5$,代入公式得$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\bar x)({y_i}-\bar y)}}}{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}}=1.23$,
所以$\hat a=\bar y-\hat b\overline{x}=0.08$
所以回归直线方程为$\hat y=1.23x+0.08$
(3)∵x=10,$\hat y=12.38$,
∴预计第10年需要支出维修费用12.38 万元.
点评 本题考查线性回归方程的求解和应用,是一个基础题,解题的关键是正确应用最小二乘法来求线性回归方程的系数.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:解答题
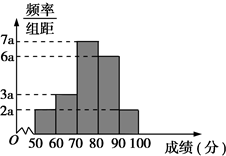 20名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.
20名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在梯形ABCD中,AB∥DC,AD⊥AB,AD=DC=1,AB=2,点P,Q分别在线段BC,CD上运动,且$\overrightarrow{DQ}$=λ$\overrightarrow{DC}$,$\overrightarrow{CP}$=(1-λ)$\overrightarrow{CB}$.
如图,在梯形ABCD中,AB∥DC,AD⊥AB,AD=DC=1,AB=2,点P,Q分别在线段BC,CD上运动,且$\overrightarrow{DQ}$=λ$\overrightarrow{DC}$,$\overrightarrow{CP}$=(1-λ)$\overrightarrow{CB}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com