
本小题满分13分)
先后随机投掷2枚正方体(六面分别标有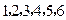 )骰子,其中
)骰子,其中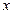 表示第
表示第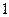 枚骰子出现的点数,
枚骰子出现的点数,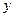 表示第
表示第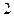 枚骰子出现的点数。
枚骰子出现的点数。
(1)求点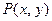 在直线
在直线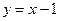 上的概率;
上的概率;
(2)求点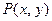 满足
满足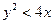 的概率。
的概率。
 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:解答题
某人一次同时抛掷两枚均匀骰子(它们的六个面分别标有点数1、2、3、4、5、6)
求:(1)两枚骰子点数相同的概率;
(2)两枚骰子点数和为5的倍数的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校高一年级共有320人,为调查高一年级学生每天晚自习自主支配学习时间(指除了完成老师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.
(1)求n的值;
(2)若高一全体学生平均每天晚自习自主支配学习时间少于45分钟,则学校需要减少作业量.根据以上抽样调查数据,学校是否需要减少作业量?
(注:统计方法中,同一组数据常用该组区间的中点值作为代表)
(3)问卷调查完成后,学校从第3组和第4组学生中利用分层抽样的方法抽取7名学生进行座谈,了解各学科的作业布置情况,并从这7人中随机抽取两名学生聘为学情调查联系人。求第3组中至少有1名学生被聘为学情调查联系人的概率。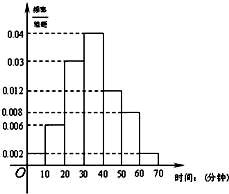
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
甲,乙,丙三个同学同时报名参加某重点高校2012年自主招生.高考前自主招生的程序为审核材料和文化测试,只有审核过关后才能参加文化测试,文化测试合格者即可获得自主招生入选资格.因为甲,乙,丙三人各有优势,甲,乙,丙三人审核过关的概率分别为0.5,0.6,0.4,审核过关后,甲,乙,丙三人文化测试合格的概率分别为0.6,0.5,0.75.
(1)求甲,乙,丙三人中只有一人通过审核的概率;
(2)设甲,乙,丙三人中获得自主招生入选资格的人数为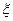 ,求随机变量
,求随机变量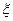 的期望.
的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
编号为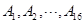 的16名篮球运动员在某次训练比赛中的得分记录如下:
的16名篮球运动员在某次训练比赛中的得分记录如下:
| 运动员编号 | 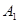 | 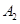 | 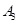 | 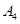 | 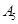 | 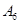 | 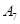 | 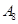 |
| 得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 |
| 运动员编号 | 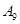 | 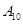 | 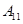 | 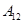 | 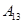 | 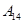 | 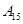 | 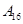 |
| 得分 | 17 | 26 | 25 | 33 | 22 | 12 | 31 | 38 |
| 区间 |  | 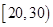 | 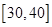 |
| 人数 | | | |
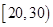 内的运动员中随机抽取2人,
内的运动员中随机抽取2人,查看答案和解析>>
科目:高中数学 来源: 题型:单选题
[2014·三门峡联考]有4位教师在同一年级的4个班中各教一个班的数学,在数学检测时要求每位教师不能在本班监考,则监考的方法有( )
| A.8种 | B.9种 | C.10种 | D.11种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com