练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    双曲线tx2-y2-1=0的一条渐近线与直线2x+y+1=0垂直，则t=________．


    分析：双曲线化成标准方程，可得它的渐近线方程为y=±x，再由一条渐近线与直线2x+y+1=0垂直，建立关于t的方程，解之即可求得实数t的值．
    解答：∵双曲线tx2-y2-1=0化成标准方程，得
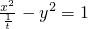
    ∴双曲线的渐近线方程为y=±x，
    ∵一条渐近线与直线2x+y+1=0垂直，而直线2x+y+1=0的斜率k=-2
    ∴×（-2）=-1，解这得t=
    故答案为：
    点评：本题给出双曲线的一条渐近线与已知直线垂直，求参数t的值，着重考查了双曲线的标准方程和简单几何性质等知识，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    双曲线tx2-y2-1=0的一条渐近线与直线2x+y+1=0垂直，则双曲线的离心率为（　　）
    A、
    		5
    2
    B、
    		5
    C、
    		3
    2
    D、
    		3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    双曲线tx2-y2-1=0的一条渐近线与直线2x+y+1=0垂直，则t=
    1
    4
    1
    4
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2006•崇文区二模）双曲线tx2-y2-1=0的一条渐近线与直线2x+y+1=0垂直，则双曲线的离心率为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2006•崇文区二模）双曲线tx2-y2-1=0的一条渐近线与直线x-2y+1=0平行，则双曲线的离心率为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    双曲线tx2-y2+1=0的一条渐近线与直线2x+y+1=0垂直，则双曲线的离心率为________.

    查看答案和解析>>

    同步练习册答案