
【题目】如图.在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() 平面ABCD,且
平面ABCD,且![]() .
.![]() ,
,![]() ,M、N分别为棱PC,PB的中点.
,M、N分别为棱PC,PB的中点.

(1)证明:A,D,M,N四点共面,且![]() 平面ADMN;
平面ADMN;
(2)求直线BD与平面ADMN所成角的正弦值.
【答案】(1) 证明见解析;(2) ![]()
【解析】
(1)先证![]() ,再证
,再证![]() ,即可得证;要证
,即可得证;要证![]() 平面ADMN,可通过求证PB垂直于ADMN中的两条交线来证明
平面ADMN,可通过求证PB垂直于ADMN中的两条交线来证明
(2)求直线BD与平面ADMN所成角,需要找出BD在平面ADMN的射影,可通过三垂线定理去进行证明
解:(1)证明因为M,N分别为PC,PB的中点,所以![]() ;
;
又因为![]() ,所以
,所以![]() .从而A,D,M,N四点共面;
.从而A,D,M,N四点共面;
因为![]() 平面ABCD,
平面ABCD,![]() 平面ABCD.所以
平面ABCD.所以![]() ,
,
又因为![]() ,
,![]() ,所以
,所以![]() 平面PAB,从而
平面PAB,从而![]() ,
,
因为![]() ,且N为PB的中点,所以
,且N为PB的中点,所以![]() ;
;
又因为![]() ,所以
,所以![]() 平面ADMN;
平面ADMN;
(2)如图,连结DN;
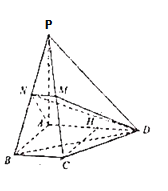
由(1)知![]() 平面ADMN,
平面ADMN,
所以,DN为直线BD在平面ADMN内的射影,且![]() ,
,
所以,![]() 即为直线BD与平面ADMN所成的角:
即为直线BD与平面ADMN所成的角:
在直角梯形ABCD内,过C作![]() 于H,则四边形ABCH为矩形;
于H,则四边形ABCH为矩形;
![]() ,在
,在![]() 中,
中,![]() ;
;
所以,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.
综上,直线BD与平面ADMN所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(1-x)+lg(1+x)+x4-2x2.
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2007全运会上两名射击运动员甲、乙在比赛中打出如下成绩:
甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;
乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;
(1)用茎叶图表示甲,乙两个成绩;并根据茎叶图分析甲、乙两人成绩;
(2)分别计算两个样本的平均数![]() 和标准差
和标准差![]() ,并根据计算结果估计哪位运动员的成绩比较稳定.
,并根据计算结果估计哪位运动员的成绩比较稳定.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】行驶中的汽车,在刹车时由于惯性作用,要继续往前滑行一段距离才能停下,这段距离叫做刹车距离,在某种路面上,某种型号的汽车的刹车距离s(m)与汽车的车速v(m/s)满足下列关系:![]() (n为常数,且
(n为常数,且![]() ),做了两次刹车实验,发现实验数据如图所示其中
),做了两次刹车实验,发现实验数据如图所示其中

(1)求出n的值;
(2)要使刹车距离不超过12.6米,则行驶的最大速度应为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为![]() .
.
(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,从A1(1,0,0),A2(2,0,0),B1(0,1,0),B2(0,2,0),C1(0,0,1),C2(0,0,2)这6个点中随机选取3个点,将这3个点及原点O两两相连构成一个“立体”,记该“立体”的体积为随机变量V(如果选取的3个点与原点在同一个平面内,此时“立体”的体积V=0).

(1)求V=0的概率;
(2)求V的分布列及数学期望E(V).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 截直线
截直线![]() 所得线段的中点坐标为
所得线段的中点坐标为![]() ,求
,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地铁换乘站设有编号为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的五个安全出口.若同时开放其中的两个安全出口,疏散1000名乘客所需的时间如下:
的五个安全出口.若同时开放其中的两个安全出口,疏散1000名乘客所需的时间如下:
安全出口编号 |
|
|
|
|
|
疏散乘客时间( | 186 | 125 | 160 | 175 | 145 |
则疏散乘客最快的一个安全出口的编号是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com