
【题目】已知数列{an}是公差不为零的等差数列,a1=1,且a2 , a4 , a8成等比数列.
(1)求数列{an}的通项公式;
(2)设数列{bn}满足:a1b1+a2b2+a3b3+…+anbn=2n+1 , n∈N* , 令cn= ![]() ,n∈N* , 求数列{cncn+1}的前n项和Sn .
,n∈N* , 求数列{cncn+1}的前n项和Sn .
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD中,底面ABCD为平行四边形,AB=3,AC=4,AD=5,SA⊥平面ABCD. 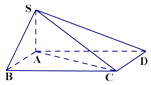
(1)证明:AC⊥平面SAB;
(2)若SA=2,求三棱锥A﹣SCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,且过点(
,且过点( ![]() ,
, ![]() ).
).
(1)求椭圆方程;
(2)设不过原点O的直线l:y=kx+m(k≠0),与该椭圆交于P、Q两点,直线OP、OQ的斜率依次为k1、k2 , 满足4k=k1+k2 , 试问:当k变化时,m2是否为定值?若是,求出此定值,并证明你的结论;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数 ![]() 在区间[﹣
在区间[﹣ ![]() ,
, ![]() ]上的图象时,列表并填入了部分数据,如表:
]上的图象时,列表并填入了部分数据,如表:
2x﹣ | ﹣ | ﹣π | ﹣ | 0 |
|
|
x | ﹣ | ﹣ | ﹣ |
|
|
|
f(x) |
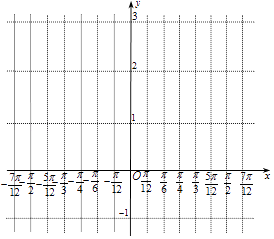
(1)请将上表数据补充完整,并在给出的直角坐标系中,画出f(x)在区间[﹣ ![]() ,
, ![]() ]上的图象;
]上的图象;
(2)求f(x)的最小值及取最小值时x的集合;
(3)求f(x)在 ![]() 时的值域.
时的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装厂生产一种服装,每件服装的成本为40元,出厂单价定为60元.该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出厂单价就降低0.02元.根据市场调查,销售商一次订购量不会超过500件.
(1)设一次订购量为x件,服装的实际出厂单价为P元,写出函数P=f(x)的表达式;
(2)当销售商一次订购多少件时,该服装厂获得的利润最大,最大利润是多少元? (服装厂售出一件服装的利润=实际出厂单价﹣成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上. 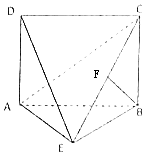
(1)求证:AE⊥BE;
(2)求三棱锥C﹣ADE的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com