
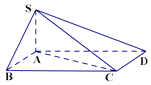
【题目】如图,四棱锥S﹣ABCD中,底面ABCD为平行四边形,AB=3,AC=4,AD=5,SA⊥平面ABCD. 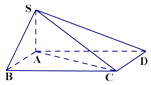
(1)证明:AC⊥平面SAB;
(2)若SA=2,求三棱锥A﹣SCD的体积.
【答案】
(1)证明:∵四棱锥S﹣ABCD中,底面ABCD为平行四边形,
AB=3,AC=4,AD=5,
∴BC2=AB2+AC2,AC⊥AB,
∵SA⊥平面ABCD,∴SA⊥AC,
∵AB∩SA=A,∴AC⊥平面SAB
(2)解: VA﹣SCD=VS﹣ACD= ![]() ,
,
∵SA⊥平面ABCD,
∴SA是三棱锥S﹣ACD的高,
S△ACD= ![]() =
= ![]() =6,
=6,
∴VA﹣SCD=VS﹣ACD
= ![]() =
= ![]() .
.
【解析】(1)推导出AC⊥AB,SA⊥AC,由此能证明AC⊥平面SAB.(2)由VA﹣SCD=VS﹣ACD , 能求出三棱锥A﹣SCD的体积.
【考点精析】利用直线与平面垂直的判定对题目进行判断即可得到答案,需要熟知一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sinxcosx+sin2x﹣
sinxcosx+sin2x﹣ ![]() .
.
(1)求f(x)的最小正周期及其对称轴方程;
(2)设函数g(x)=f( ![]() +
+ ![]() ),其中常数ω>0,|φ|<
),其中常数ω>0,|φ|< ![]() . (i)当ω=4,φ=
. (i)当ω=4,φ= ![]() 时,函数y=g(x)﹣4λf(x)在[
时,函数y=g(x)﹣4λf(x)在[ ![]() ,
, ![]() ]上的最大值为
]上的最大值为 ![]() ,求λ的值;
,求λ的值;
(ii)若函数g(x)的一个单调减区间内有一个零点﹣ ![]() ,且其图象过点A(
,且其图象过点A( ![]() ,1),记函数g(x)的最小正周期为T,试求T取最大值时函数g(x)的解析式.
,1),记函数g(x)的最小正周期为T,试求T取最大值时函数g(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=asin 2x+bcos 2x,其中a,b∈R,ab≠0.若f(x)≤|f( ![]() )|对一切x∈R恒成立,则以下结论正确的是(写出所有正确结论的编号). ①
)|对一切x∈R恒成立,则以下结论正确的是(写出所有正确结论的编号). ① ![]() ;②
;② ![]() ≥
≥ ![]() ;
;
③f(x)的单调递增区间是(kπ+ ![]() ,kπ+
,kπ+ ![]() )(k∈Z);
)(k∈Z);
④f(x)既不是奇函数也不是偶函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学高三年级甲乙两班各10名同学,测量出他们的身高(单位:cm),获得身高数据的茎叶图如图.其中甲班有一个数据被污损.
(Ⅰ)若已知甲班同学身高平均数为170cm,求污损处的数据;
(Ⅱ)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax﹣ ![]() (a,b∈N*),f(1)=
(a,b∈N*),f(1)= ![]() 且f(2)<2.
且f(2)<2.
(Ⅰ)求a,b的值;
(Ⅱ)判断并证明函数y=f(x)在区间(﹣1,+∞)上的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x2﹣3x+1, ![]() ,(A≠0)
,(A≠0)
(1)当0≤x≤ ![]() 时,求y=f(sinx)的最大值;
时,求y=f(sinx)的最大值;
(2)若对任意的x1∈[0,3],总存在x2∈[0,3],使f(x1)=g(x2)成立,求实数A的取值范围;
(3)问a取何值时,方程f(sinx)=a﹣sinx在[0,2π)上有两解?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(2x﹣ ![]() )的图象,只需把正弦曲线y=sinx上所有点( )
)的图象,只需把正弦曲线y=sinx上所有点( )
A.向右平移 ![]() 个单位长度,再将所得图象上的点横坐标缩短为原来的
个单位长度,再将所得图象上的点横坐标缩短为原来的 ![]() 倍,纵坐标不变
倍,纵坐标不变
B.向左平移 ![]() 个单位长度,再将所得图象上的点横坐标缩短为原来的
个单位长度,再将所得图象上的点横坐标缩短为原来的 ![]() 倍,纵坐标不变
倍,纵坐标不变
C.向右平移 ![]() 个单位长度,再将所得图象上的点横坐标伸长为原来的2倍,纵坐标不变
个单位长度,再将所得图象上的点横坐标伸长为原来的2倍,纵坐标不变
D.向左平移 ![]() 个单位长度,再将所得图象上的点横坐标缩短为原来的2倍,纵坐标不变
个单位长度,再将所得图象上的点横坐标缩短为原来的2倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是公差不为零的等差数列,a1=1,且a2 , a4 , a8成等比数列.
(1)求数列{an}的通项公式;
(2)设数列{bn}满足:a1b1+a2b2+a3b3+…+anbn=2n+1 , n∈N* , 令cn= ![]() ,n∈N* , 求数列{cncn+1}的前n项和Sn .
,n∈N* , 求数列{cncn+1}的前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com