
 ���������˵�ΪA��B�������϶˵�ΪC��
���������˵�ΪA��B�������϶˵�ΪC��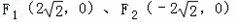 ����M����Բ���˶�������ABM��������Ϊ3ʱ��������Բ���̣�
����M����Բ���˶�������ABM��������Ϊ3ʱ��������Բ���̣�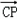 ��ֱ��
��ֱ��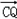 ����P��Q����Բ�ϣ�������y�����Ƿ����һ��Tʹ��ֱ��TP��б����TQ��б��֮��Ϊ��ֵ��������ڣ��ҳ���T������Ͷ�ֵ����������ڣ�˵�����ɣ�
����P��Q����Բ�ϣ�������y�����Ƿ����һ��Tʹ��ֱ��TP��б����TQ��б��֮��Ϊ��ֵ��������ڣ��ҳ���T������Ͷ�ֵ����������ڣ�˵�����ɣ�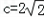 ��
�� ��
��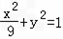
 ��
��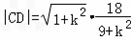
 ��
��
 ��
�� ��
��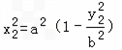 ��
�� ��
��

 ��Ϊ��ֵ����
��Ϊ��ֵ����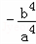


 ��Ч���ܿ�ʱ��ҵϵ�д�
��Ч���ܿ�ʱ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
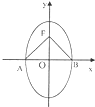 ��ͼ��ʾ����֪��Բ����Ϊ
��ͼ��ʾ����֪��Բ����Ϊ| y2 |
| a2 |
| x2 |
| b2 |
| 3 |
| 2 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��08�곤����ѧ��ģ������13�֣� ��֪��Բ����Ϊ![]() ���������˵�Ϊ
���������˵�Ϊ![]() �������϶˵�Ϊ
�������϶˵�Ϊ![]() ��
��
��1������Բ��������Ϊ![]() ����
����![]() ����Բ���˶�����
����Բ���˶�����![]() ��������Ϊ3ʱ��������Բ���̣�
��������Ϊ3ʱ��������Բ���̣�
��2�����ڣ�1���е���Բ���̣�����![]() Ϊֱ�Ƕ�����ڽ�����Բ�ĵ���ֱ��������
Ϊֱ�Ƕ�����ڽ�����Բ�ĵ���ֱ��������![]() ����ֱ��
����ֱ��![]() ��б��Ϊ
��б��Ϊ![]() ������
������![]() ��ֵ��
��ֵ��
��3����![]() ����
����![]() ��ֱ��
��ֱ��![]() ����
����![]() ����Բ�ϣ�������
����Բ�ϣ�������![]() �����Ƿ���ڵ�
�����Ƿ���ڵ�![]() ��ʹ��ֱ��
��ʹ��ֱ��![]() ��б����
��б����![]() ��б��֮��Ϊ��ֵ��������ڣ��ҳ�һ����
��б��֮��Ϊ��ֵ��������ڣ��ҳ�һ����![]() �����꣬��������ڣ�˵�����ɣ�
�����꣬��������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2008���Ϻ����������߿���ѧ��ģ�Ծ������ƣ��������棩 ���ͣ������
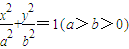 ���������˵�ΪA��B�������϶˵�ΪC��
���������˵�ΪA��B�������϶˵�ΪC��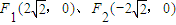 ����M����Բ���˶�������ABM��������Ϊ3ʱ��������Բ���̣�
����M����Բ���˶�������ABM��������Ϊ3ʱ��������Բ���̣�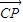 ��ֱ��
��ֱ��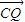 ����P��Q����Բ�ϣ�������y�����Ƿ����һ��Tʹ��ֱ��TP��б����TQ��б��֮��Ϊ��ֵ��������ڣ��ҳ���T������Ͷ�ֵ����������ڣ�˵�����ɣ�
����P��Q����Բ�ϣ�������y�����Ƿ����һ��Tʹ��ֱ��TP��б����TQ��б��֮��Ϊ��ֵ��������ڣ��ҳ���T������Ͷ�ֵ����������ڣ�˵�����ɣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com