
 ,求f(x).
,求f(x).科目:高中数学 来源:2012-2013学年浙江省湖州八中高二(下)开学数学试卷(解析版) 题型:解答题
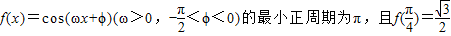 .
.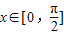 ,求f(x)的取值范围.
,求f(x)的取值范围.查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市通州区潞河中学高一(上)期末数学试卷(解析版) 题型:解答题
 .
. ,求f(x)的最大值及最小值.
,求f(x)的最大值及最小值.查看答案和解析>>
科目:高中数学 来源:2009-2010学年北京市昌平一中高三(上)11月月考数学试卷(理科)(解析版) 题型:解答题
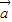 =(cosx,2cosx),向量
=(cosx,2cosx),向量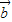 =(2cosx,sin(π-x)),若f(x)=
=(2cosx,sin(π-x)),若f(x)=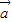 •
•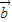 +1.
+1.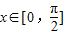 ,求f(x)的最大值和最小值.
,求f(x)的最大值和最小值.查看答案和解析>>
科目:高中数学 来源:2011年广东省深圳市高考数学二模试卷(理科)(解析版) 题型:解答题
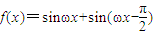 ,x∈R.
,x∈R. ,求f(x)的最大值及相应的x的集合;
,求f(x)的最大值及相应的x的集合;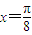 是f(x)的一个零点,且0<ω<10,求ω的值和f(x)的最小正周期.
是f(x)的一个零点,且0<ω<10,求ω的值和f(x)的最小正周期.查看答案和解析>>
科目:高中数学 来源:2009-2010学年北京大学附中高三(下)数学练习试卷3(文科)(解析版) 题型:解答题
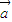 =(cosx,2cosx),向量
=(cosx,2cosx),向量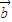 =(2cosx,sin(π-x)),若f(x)=
=(2cosx,sin(π-x)),若f(x)=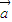 •
• +1.
+1.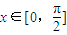 ,求f(x)的最大值和最小值.
,求f(x)的最大值和最小值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com