
分析 以面积为测度,建立方程,即可求出圆周率π的近似值.
解答 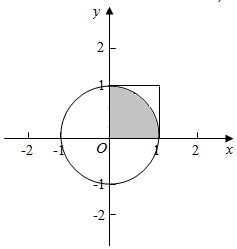 解:由题意,两数的平方和小于1,对应的区域的面积为$\frac{1}{4}$π•12,从区间[0,1]随机抽取2n个数x1,x2,…,xn,y1,y2,…,yn,构成n个数对(x1,y1),(x2,y2),…,(xn,yn),对应的区域的面积为12,
解:由题意,两数的平方和小于1,对应的区域的面积为$\frac{1}{4}$π•12,从区间[0,1]随机抽取2n个数x1,x2,…,xn,y1,y2,…,yn,构成n个数对(x1,y1),(x2,y2),…,(xn,yn),对应的区域的面积为12,
∴$\frac{m}{n}=\frac{\frac{1}{4}π•{1}^{2}}{{1}^{2}}$,∴π=$\frac{4m}{n}$.
故答案为:$\frac{4m}{n}$.
点评 古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积和体积的比值得到.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
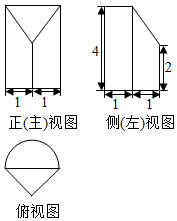 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | 3(π+1) | B. | 4π+1 | C. | π+$\frac{8}{3}$ | D. | 2π+$\frac{10}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-y=0 | B. | x-2y+3=0 | C. | 2x+y-4=0 | D. | x+2y-5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com