
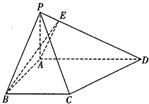
 在四棱锥P-ABCD中,底面ABCD是一直角梯,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,PA⊥底面ABCD,PD与底面成30°角.
在四棱锥P-ABCD中,底面ABCD是一直角梯,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,PA⊥底面ABCD,PD与底面成30°角.| 分析:解法一: (1)欲证直线与直线垂直,可用先证直线与平面垂直.∵BA⊥AD,BA⊥PA,∴BA⊥平面PAD.∴PD⊥BA.又∵PD⊥AE,∴PD⊥平面BAE,∴PD⊥BE. (2)求异面直线所成的角,可以做适当的平移,把异面直线转化为相交直线,然后在相关的三角形中借助正弦或余弦定理解出所求的角.平移时主要是根据中位线和中点条件,或者是特殊的四边形,三角形等.过点E作EM∥CD交PC于M,连接AM,则AE与ME所成角即为AE与CD所成角. (3)二面角的度量关键在于找出它的平面角,构造平面角常用的方法就是三垂线法.延长AB与DC相交于G点,连PG,则面PAB与面PCD的交线为PG,易知CB⊥平面PAB,过B作BF⊥PG于F点,连CF,则CF⊥PG,∴∠CFB为二面角C-PG-A的平面角 解法二: 在含有直线与平面垂直垂直的条件的棱柱、棱锥、棱台中,也可以建立空间直角坐标系,设定参量求解.这种解法的好处就是:1、解题过程中较少用到空间几何中判定线线、面面、线面相对位置的有关定理,因为这些可以用向量方法来解决.2、即使立体感稍差一些的学生也可以顺利解出,因为只需画个草图以建立坐标系和观察有关点的位置即可.则A(0,0,0),B(a,0,0),E(0,
(1)
(2)由(1)知,
(3)利用平面PAB与平面PCD的法向量所成的角,去求平面PAB与平面PCD所成的锐二面角的正切值. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 解答:解法一:(1)∵∠BAD=90°,∴BA⊥AD ∵PA⊥底面ABCD,BA⊥PA.又∵PA∩AD=A,BA⊥PA.又∵PA∩AD=A, ∴BA⊥平面PAD. ∵PD?平面PAD. ∴PD⊥BA.又∵PD⊥AE,且BA∩AE=A, ∴PD⊥平面BAE ∴PD⊥BE,即BE⊥PD.(4分) (2)过点E作EM∥CD交PC于M,连接AM,则AE与ME所成角即为AE与CD所成角 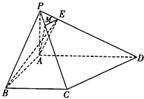 ∵PA⊥底面ABCD,且PD与底面ABCD成30°角. ∴∠PDA=30°. ∴在Rt△PAD中,∠PAD=90°,∠PDA=30°,AD=2a ∴PA=
∴AE=
∵PE=
∴ME=
连接AC ∵在△ACD中AD=2a,AC=
AD2=AC2+CD2 ∴∠ACD=90°,∴CD⊥AC,∴ME⊥AC 又∵PA⊥底面ABCD, ∴PA⊥CD,∴ME⊥PA. ∴ME⊥平面PAC.∵MA?平面PAC, ∵ME⊥AM. ∴在Rt△AME中,cos∠MEA=
 ∴异面直线AE与CD所成角的余弦值为
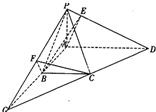
(9分) (3)延长AB与DC相交于G点,连PG,则面PAB 与面PCD的交线为PG,易知CB⊥平面PAB,过B作BF⊥PG于F点,连CF,则CF⊥PG, ∴∠CFB为二面角C-PG-A的平面角, ∵CB∥
∴GB=AB=a,∠PDA=30°,PA=
∴∠PGA=30°, ∴BF=
∴平面PAB与平面PCD所成的二面角的正切值为2.(14分) 解法二:(1)如图建立空间直角坐标系, 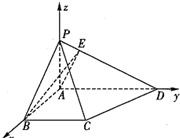 则A(0,0,0),B(a,0,0),E(0,
D(0,2a,0),P(0,0,
∴
∴
∴BE⊥PD(4分) (2)由(1)知,
则cosθ=
∴异面直线AE与CD所成角的余统值为
(3)易知,CB⊥AB,CB⊥PA, 则CB⊥平面PAB.,∴
又设平面PCD的一个法向量为
则
∴由
得
∴
令y=1,,∴
设向量
则cosθ=
|


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点
如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,
(2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com