解:(Ⅰ)∵b
2+c
2-a
2=bc,
∴由余弦定理得:cosA=

=
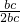
=

,
∵0<A<π,
∴A=

;
(Ⅱ)f(x)=

sin

cos

+cos
2
=

sinx+

cosx+

=sin(x+

)+

,
∴f(B)=sin(B+

)+

,
∵A=

,∴B∈(0,

),
∴

<B+

<

,
∴当B+

=

,即B=

时,f(B)有最大值是

,
又∵A=

,∴C=

,
∴△ABC为等边三角形;
(Ⅲ)∵ω=1,
∴T=2π;
∵-1≤sin(x+

)≤1,
∴-

≤sin(x+

)+

≤

,
则函数的最大值为

,最小值为-

.
分析:(Ⅰ)利用余弦定理表示出cosA,将已知的等式代入求出cosA的值,由A为三角形的内角,利用特殊角的三角函数值即可求出A的度数;
(Ⅱ)将函数解析式两项分别利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式化为一个角的正弦函数,表示出f(B),根据A的度数,得出B的范围,求出这个角的范围,根据正弦函数的图象与性质求出f(B)取得最大值时B的度数,可得出此时C的度数,进而判断出此三角形为等边三角形;
(Ⅲ)由第二问得出的函数解析式,找出ω的值,代入周期公式,即可求出函数的最小正周期;根据正弦函数的值域为[-1,1],求出函数的值域,即可得到函数的最小值与最大值.
点评:此题考查了余弦定理,二倍角的正弦、余弦函数公式,正弦函数的定义域与值域,以及三角函数的周期性及其求法,熟练掌握定理及公式是解本题的关键.

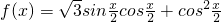 ,当f(B)取最大值
,当f(B)取最大值 时,判断△ABC的形状;
时,判断△ABC的形状; =
=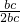 =
= ,
, ;
; sin
sin cos
cos +cos2
+cos2 =
= sinx+
sinx+ cosx+
cosx+ =sin(x+
=sin(x+ )+
)+ ,
, )+
)+ ,
, ,∴B∈(0,
,∴B∈(0, ),
), <B+
<B+ <
< ,
, =
= ,即B=
,即B= 时,f(B)有最大值是
时,f(B)有最大值是 ,
, ,∴C=
,∴C= ,
, )≤1,
)≤1, ≤sin(x+
≤sin(x+ )+
)+ ≤
≤ ,
, ,最小值为-
,最小值为- .
.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案