
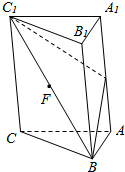
 如图,在正棱柱ABC-A1B1C1中,E,F分别为线段AA1,C1B的中点,求证:EF∥平面ABC.
如图,在正棱柱ABC-A1B1C1中,E,F分别为线段AA1,C1B的中点,求证:EF∥平面ABC. 分析 根据图形,取BC的中点G,连接AG、FG,证明四边形AEFG是平行四边形,得出EF∥AG,从而证明EF∥平面ABC.
解答  证明:如图所示,
证明:如图所示,
取BC的中点G,连接AG、FG,
∵E,F分别为AA1,C1B的中点,
∴FG∥CC1,且FG=$\frac{1}{2}$CC1;
AE=$\frac{1}{2}$AA1,AA1∥CC1,AA1=CC1,
∴AE∥CC1,且AE=$\frac{1}{2}$CC1;
∴AE∥FG,且AE=FG,
∴四边形AEFG是平行四边形,
∴EF∥AG;
又EF?平面ABC,AG?平面ABC,
∴EF∥平面ABC.
点评 本题考查了空间中的直线与平面平行的判断问题,也考查了空间想象能力与逻辑推理能力的应用问题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>1 | B. | a≤1 | C. | a<-1 | D. | a≤-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
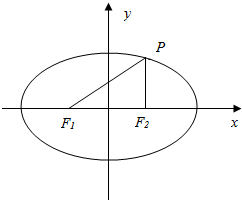 如图,$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上任一点,F1,F2为椭圆的左、右焦点,求|PF1|的 最大值和最小值.
如图,$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上任一点,F1,F2为椭圆的左、右焦点,求|PF1|的 最大值和最小值.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com