
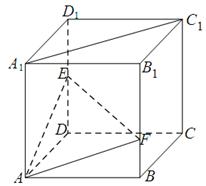
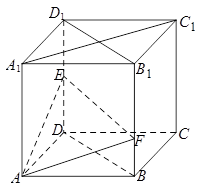
如图,在棱长为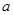 的正方体
的正方体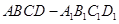 中,点
中,点 是棱
是棱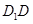 的中点,点
的中点,点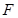 在棱
在棱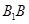 上,且满足
上,且满足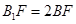 .
.
(1)求证: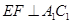 ;
;
(2)在棱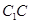 上确定一点
上确定一点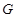 ,使
,使 、
、 、
、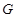 、
、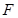 四点共面,并求此时
四点共面,并求此时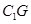 的长;
的长;
(3)求平面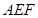 与平面
与平面 所成二面角的余弦值.
所成二面角的余弦值.
(1)详见解析;(2)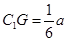 ;(3)
;(3)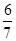 .
.
解析试题分析:本题有两种方法,第一种是传统方法:(1)连接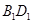 ,先由正方体的性质得到
,先由正方体的性质得到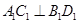 ,以及
,以及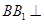 平面
平面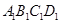 ,从而得到
,从而得到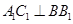 ,利用直线与平面垂直的判定定理可以得到
,利用直线与平面垂直的判定定理可以得到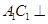 平面
平面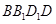 ,于是得到
,于是得到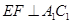 ;(2)假设四点
;(2)假设四点 、
、 、
、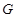 、
、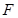 四点共面,利用平面与平面平行的性质定理得到
四点共面,利用平面与平面平行的性质定理得到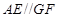 ,
,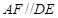 ,于是得到四边形
,于是得到四边形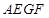 为平行四边形,从而得到
为平行四边形,从而得到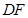 的长度,再结合勾股定理得到
的长度,再结合勾股定理得到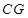 的长度,最终得到
的长度,最终得到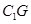 的长度;(3)先延长
的长度;(3)先延长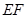 、
、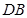 交于点
交于点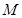 ,连接
,连接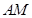 ,找出由平面
,找出由平面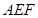 与平面
与平面 所形成的二面角的棱
所形成的二面角的棱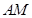 ,借助
,借助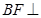 平面
平面 ,从点
,从点 在平面
在平面 内作
内作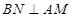 ,连接
,连接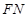 ,利用三垂线法得到
,利用三垂线法得到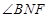 为平面
为平面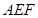 与平面
与平面 所形成的二面角的的平面角,然后在直角
所形成的二面角的的平面角,然后在直角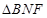 中计算
中计算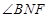 的余弦值;
的余弦值;
第二种方法是空间向量法:(1)以点 为坐标原点,
为坐标原点,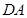 、
、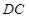 、
、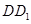 所在直线分别为
所在直线分别为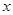 轴、
轴、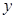 轴、
轴、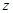 轴建立空间直角坐标系,确定
轴建立空间直角坐标系,确定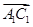 与
与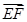 的坐标,利用
的坐标,利用 来证明
来证明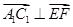 ,进而证明
,进而证明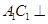
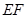 ;(2)先利用平面与平面平行的性质定理得到
;(2)先利用平面与平面平行的性质定理得到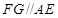 ,然后利用空间向量共线求出点
,然后利用空间向量共线求出点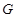 的坐标,进而求出
的坐标,进而求出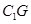 的长度;(3)先求出平面
的长度;(3)先求出平面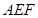 和平面
和平面 的法向量,结合图形得到由平面
的法向量,结合图形得到由平面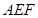 和平面
和平面 所形成的二面角为锐角,最后再利用两个平面的法向量的夹角来进行计算.
所形成的二面角为锐角,最后再利用两个平面的法向量的夹角来进行计算.
试题解析:(1)如下图所示,连接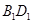 ,
,
由于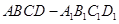 为正方体,所以四边形
为正方体,所以四边形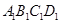 为正方形,所以
为正方形,所以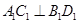 ,
,
且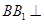 平面
平面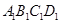 ,
,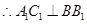 ,
,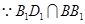 ,
,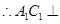 平面
平面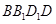 ,
,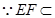 平面
平面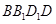 ,
,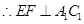 ;
;
(2)如下图所示,假设 、
、 、
、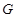 、
、


科目:高中数学 来源: 题型:解答题
如图所示,已知三棱柱ABC A1B1C1,
A1B1C1,
(1)若M、N分别是AB,A1C的中点,求证:MN∥平面BCC1B1;
(2)若三棱柱ABC A1B1C1的各棱长均为2,∠B1BA=∠B1BC=60°,P为线段B1B上的动点,当PA+PC最小时,求证:B1B⊥平面APC.
A1B1C1的各棱长均为2,∠B1BA=∠B1BC=60°,P为线段B1B上的动点,当PA+PC最小时,求证:B1B⊥平面APC.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,在直三棱柱ABCA1B1C1中,D、E分别为AA1、CC1的中点,AC⊥BE,点F在线段AB上,且AB=4AF.若M为线段BE上一点,试确定M在线段BE上的位置,使得C1D∥平面B1FM.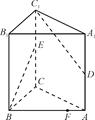
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,四边形EFGH所在平面为三棱锥A-BCD的一个截面,四边形EFGH为平行四边形.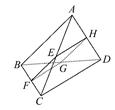
(1)求证:AB∥平面EFGH,CD∥平面EFGH.
(2)若AB=4,CD=6,求四边形EFGH周长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知四棱锥P-ABCD的底面为直角梯形,AB∥CD,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=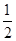 AB=1,M是PB的中点.
AB=1,M是PB的中点.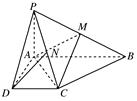
(1)求证:AM=CM;
(2)若N是PC的中点,求证:DN∥平面AMC.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,正方形ABCD所在的平面与三角形CDE所在的平面交于CD,AE⊥平面CDE,且AB=2AE.
(1)求证:AB∥平面CDE;
(2)求证:平面ABCD⊥平面ADE.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD的中点,AB=2,∠BAD=60°.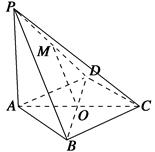
(1)求证:OM∥平面PAB;
(2)求证:平面PBD⊥平面PAC;
(3)当四棱锥P-ABCD的体积等于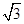 时,求PB的长.
时,求PB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com