练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知命题，；命题q：函数有两个零点．

    （1）若为假命题，求实数的取值范围；

    （2）若为真命题，为假命题，求实数的取值范围．

    【答案】（1）；（2）．

    【解析】

    先分别求出p为真、q为真时，m的取值范围，（1）若为假命题，可知p，q均为假命题，进而可求得m的取值范围；（2）若为真命题，为假命题，可知p，q一真一假，进而可求得m的取值范围.

    若p为真，令，问题转化为求函数的最小值，

    ，解得，

    函数在上单调递减，在上单调递增，

    故，故．

    若q为真，则，即或．

    （1）若为假命题．则p，q均为假命题，实数m的取值范围为.

    （2）若为真命题，为假命题，则p，q一真一假．

    若p真q假，则实数m满足，即；

    若p假q真，则实数m满足或．

    综上所述，实数m的取值范围为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知二次函数满足，且.

    （1）求的解析式；

    （2）设函数，当时，求的最小值；

    （3）设函数，若对任意，总存在，使得成立，求m的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在一次人才招聘会上，有一家公司的招聘员告诉你，“我们公司的收入水平很高”“去年，在50名员工中，最高年收入达到了200万，员工年收人的平均数是10万"，而你的预期是获得9万元年薪.

    （1）你是否能够判断年薪为9万元的员工在这家公司算高收入者？

    （2）如果招聘员继续告诉你，“员工年收入的变化范围是从3万到200万”，这个信息是否足以使你作出自己是否受聘的决定？为什么？

    （3）如果招聘员继续给你提供了如下信息，员工收人的第一四分位数为4.5万，第三四分位数为9.5万，你又该如何使用这条信息来作出是否受聘的决定？

    （4）根据（3）中招聘员提供的信息，你能估计出这家公司员工收入的中位数是多少吗？为什么平均数比估计出的中位数高很多？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=3ax2﹣2（a+c）x+c（a＞0，a，c∈R）

    （1）设a＞c＞0，若f（x）＞c2﹣2c+a对x∈[1，+∞]恒成立，求c的取值范围；

    （2）函数f（x）在区间（0，1）内是否有零点，有几个零点？为什么？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥中，，//，，为正三角形. 若，且与底面所成角的正切值为.

    （1）证明：平面平面；

    （2）是线段上一点，记（），是否存在实数，使二面角的余弦值为？若存在，求出的值；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】喜羊羊家族的四位成员与灰太狼、红太狼进行谈判，通过谈判他们握手言和，准备一起照合影像（排成一排）.

    （1）要求喜羊羊家族的四位成员必须相邻，有多少种排法？

    （2）要求灰太狼、红太狼不相邻，有多少种排法？

    （3）记灰太狼和红太狼之间的喜羊羊家族的成员个数为，求的概率分布表和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图设计一幅矩形宣传画，要求画面面积为4840，画面上下边要留8cm空白，左右要留5cm空白，怎样确定画面高与宽的尺寸，才能使宣传画所用纸张面积最小？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】【选修4－5：不等式选讲】

    已知函数

    （Ⅰ）求不等式

    （Ⅱ）若的图像与直线围成图形的面积不小于14，求实数a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点是椭圆C：上的一点，椭圆C的离心率与双曲线的离心率互为倒数，斜率为直线l交椭圆C于B，D两点，且A、B、D三点互不重合．

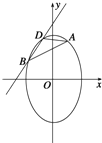
    （1）求椭圆C的方程；

    （2）若分别为直线AB，AD的斜率，求证：为定值。

    查看答案和解析>>

    同步练习册答案