
【题目】已知点![]() 是椭圆C:
是椭圆C:![]() 上的一点,椭圆C的离心率与双曲线
上的一点,椭圆C的离心率与双曲线![]() 的离心率互为倒数,斜率为
的离心率互为倒数,斜率为![]() 直线l交椭圆C于B,D两点,且A、B、D三点互不重合.
直线l交椭圆C于B,D两点,且A、B、D三点互不重合.
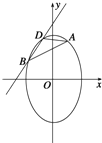
(1)求椭圆C的方程;
(2)若![]() 分别为直线AB,AD的斜率,求证:
分别为直线AB,AD的斜率,求证:![]() 为定值。
为定值。
【答案】(1)![]() (2)详见解析
(2)详见解析
【解析】
(1)根据椭圆的定义和几何性质,建立方程,即可求椭圆C的方程;
(2)设直线BD的方程为![]() ,代入椭圆方程,设D(x1,y1),B(x2,y2),直线AB、AD的斜率分别为:
,代入椭圆方程,设D(x1,y1),B(x2,y2),直线AB、AD的斜率分别为:![]() ,则
,则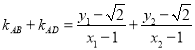 ,由此导出结果.
,由此导出结果.
(1)由题意,可得e=![]() =
=![]() ,代入A(1,
,代入A(1,![]() )得
)得![]() ,
,
又![]() ,解得
,解得![]() ,
,
所以椭圆C的方程![]() .
.
(2)证明:设直线BD的方程为y=![]() x+m,
x+m,
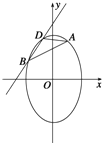
又A、B、D三点不重合,∴![]() ,
,
设D(x1,y1),B(x2,y2),
则由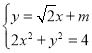 得4x2+2
得4x2+2![]() mx+m2-4=0
mx+m2-4=0
所以△=-8m2+64>0,所以![]() <m<
<m<![]() .
.
x1+x2=-![]() m,
m,![]()
设直线AB、AD的斜率分别为:kAB、kAD,
则kAD+kAB=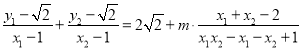
=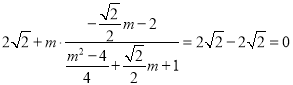
所以kAD+kAB=0,即直线AB,AD的斜率之和为定值.


科目:高中数学 来源: 题型:
【题目】下列问题中,最适合用分层随机抽样抽取样本的是( )
A.从10名同学中抽取3人参加座谈会
B.某社区有500个家庭,其中高收入的家庭125个,中等收入的家庭280个,低收入的家庭95个,为了了解生活购买力的某项指标,要从中抽取一个容量为100的样本
C.从1000名工人中,抽取100名调查上班途中所用时间
D.从生产流水线上,抽取样本检查产品质量
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个命题:
(1)命题![]() ,使得
,使得![]() ,则
,则![]() ,都有
,都有![]() ;
;
(2)已知函数f(x)=|log2x|,若a≠b,且f(a)=f(b),则ab=1;
(3)若平面α内存在不共线的三点到平面β的距离相等,则平面α平行于平面β;
(4)已知定义在![]() 上的函数
上的函数![]() 满足条件
满足条件![]() ,且函数
,且函数![]() 为奇函数,则函数
为奇函数,则函数![]() 的图象关于点
的图象关于点![]() 对称.
对称.
其中真命题的序号为______________.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市化工厂三个车间共有工人1 000名,各车间男、女工人数如下表:
第一车间 | 第二车间 | 第三车间 | |
女工 | 173 | 100 | y |
男工 | 177 | x | z |
已知在全厂工人中随机抽取1名,抽到第二车间男工的可能性是0. 15.
(1)求x的值;
(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 过点
过点![]() ,且与抛物线
,且与抛物线![]() 相交于
相交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,其中点
,其中点![]() 在第四象限,
在第四象限,![]() 为坐标原点.
为坐标原点.
(Ⅰ)当![]() 是
是![]() 中点时,求直线
中点时,求直线![]() 的方程;
的方程;
(Ⅱ)以![]() 为直径的圆交直线
为直径的圆交直线![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有编号为1,2,3,4,5的五个小球和编号为1,2,3,4,5的五个盒子,现将这五个小球放入5个盒子中.
(1)若没有一个盒子空着,但球的编号与盒子编号不全相同,有多少种投放方法?
(2)每个盒子内投放一球,并且至少有两个球的编号与盒子编号是相同的,有多少种投放方法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其导函数为
,其导函数为![]()
![]() 当
当![]() 时,若函数
时,若函数![]() 在R上有且只有一个零点,求实数a的取值范围;
在R上有且只有一个零点,求实数a的取值范围;
![]() 设
设![]() ,点
,点![]() 是曲线
是曲线![]() 上的一个定点,是否存在实数
上的一个定点,是否存在实数![]() 使得
使得![]() 成立?并证明你的结论.
成立?并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com