
【题目】在平面直角坐标系中,已知三点A(-1,0)、B(t,2)、C(2,1),t∈R,O为坐标原点
(I)若△ABC是∠B为直角的直角三角形,求t的值
(Ⅱ)若四边形ABCD是平行四边形,求![]() 的最小值
的最小值
 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:高中数学 来源: 题型:
【题目】某车间的一台机床生产出一批零件,现从中抽取8件,将其编为![]() ,
, ![]() ,…,
,…, ![]() ,测量其长度(单位:
,测量其长度(单位: ![]() ),得到如表中数据:
),得到如表中数据:
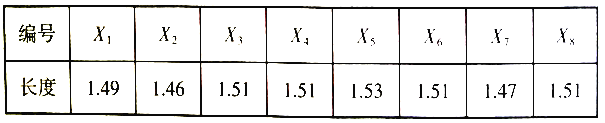
其中长度在区间![]() 内的零件为一等品.
内的零件为一等品.
(1)从上述8个零件中,随机抽取一个,求这个零件为一等品的概率;
(2)从一等品零件中,随机抽取3个.
①用零件的编号列出所有可能的抽取结果;
②求这3个零件长度相等的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一条光线从点(﹣2,﹣3)射出,经y轴反射后与圆(x+3)2+(y﹣2)2=1相切,则反射光线所在直线的斜率为( )
A.﹣ ![]() 或﹣
或﹣ ![]()
B.﹣ ![]() 或﹣
或﹣ ![]()
C.﹣ ![]() 或﹣
或﹣ ![]()
D.﹣ ![]() 或﹣
或﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() 的左、右焦点分别为F1、F2 , 离心率
的左、右焦点分别为F1、F2 , 离心率 ![]() ,P为椭圆E上的任意一点(不含长轴端点),且△PF1F2面积的最大值为1.
,P为椭圆E上的任意一点(不含长轴端点),且△PF1F2面积的最大值为1.
(Ⅰ)求椭圆E的方程;
(Ⅱ)已知直x﹣y+m=0与椭圆E交于不同的两点A,B,且线AB的中点不在圆 ![]() 内,求m的取值范围.
内,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知直线l1:4x﹣3y+6=0和直线l2:x=﹣1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是( )
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的方程:x2+y2﹣2x﹣4y+m=0
(1)求m的取值范围;
(2)圆C与直线x+2y﹣4=0相交于M,N两点,且OM⊥ON(O为坐标原点),求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“互联网+交通”模式的迅猛发展,“共享自行车”在很多城市相继出现.某运营公司为了了解某地区用户对其所提供的服务的满意度,随机调查了40个用户,得到用户的满意度评分如下:

用系统抽样法从40名用户中抽取容量为10的样本,且在第一分段里随机抽到的评分数据为92.
(1)请你列出抽到的10个样本的评分数据;
(2)计算所抽到的10个样本的均值![]() 和方差
和方差![]() ;
;
(3)在(2)条件下,若用户的满意度评分在![]() 之间,则满意度等级为“
之间,则满意度等级为“![]() 级”.试应用样本估计总体的思想,估计该地区满意度等级为“
级”.试应用样本估计总体的思想,估计该地区满意度等级为“![]() 级”的用户所占的百分比是多少?(精确到
级”的用户所占的百分比是多少?(精确到![]() )
)
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ﹣k ln x,k>0.
﹣k ln x,k>0.
(1)求f(x)的单调区间和极值;
(2)证明:若f(x)存在零点,则f(x)在区间(1, ![]() ]上仅有一个零点.
]上仅有一个零点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com