
【题目】已知函数 ![]() .
.
(1)判断函数![]() 的奇偶性;
的奇偶性;
(2)求证:函数![]() 在
在![]() 为单调增函数;
为单调增函数;
(3)求满足![]() 的
的![]() 的取值范围.
的取值范围.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
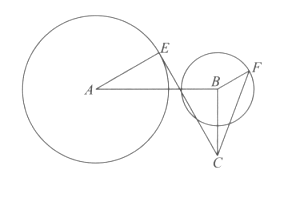
【题目】如图,已知AB⊥BC,AB=![]() BC=
BC=![]() a,a∈[1,3],圆A是以A为圆心、半径为2的圆,圆B是以B为圆心、半径为1的圆,设点E、F分别为圆A、圆B上的动点,
a,a∈[1,3],圆A是以A为圆心、半径为2的圆,圆B是以B为圆心、半径为1的圆,设点E、F分别为圆A、圆B上的动点, ![]() ∥
∥![]() (且
(且![]() 与
与![]() 同向),设∠BAE=θ(θ∈[0,π]).
同向),设∠BAE=θ(θ∈[0,π]).
(I)当a= ![]() ,且θ=
,且θ=![]() 时,求
时,求![]() 的值;
的值;
(Ⅱ)用a,θ表示出![]() ,并给出一组a,θ的值,使得
,并给出一组a,θ的值,使得![]() 最小.
最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(2x﹣ ![]() )的图象,只需将函数y=sin2x的图象上所有的点( )
)的图象,只需将函数y=sin2x的图象上所有的点( )
A.向左平移 ![]() 个单位
个单位
B.向左平移 ![]() 个单位
个单位
C.向右平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读下面材料:
根据两角和与差的正弦公式,有
![]() ------①
------①
![]() ------②
------②
由①+② 得![]() ------③
------③
令![]() 有
有![]()
代入③得![]() .
.
(Ⅰ)类比上述推证方法,根据两角和与差的余弦公式,证明:
![]() ;
;
(Ⅱ)若![]() 的三个内角
的三个内角![]() 满足
满足![]() ,试判断
,试判断![]() 的形状.
的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某中草药材的销售量与年份有关,下表是近五年的部分统计数据:
年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
销售量(吨) | 114 | 115 | 116 | 116 | 114 |
(1)利用所给数据求年销售量![]() 与年份
与年份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)利用(1)中所求出的直线方程预测该地2018年的中草药的销售量.
参考公式: 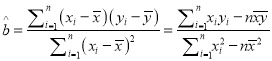 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知三点A(-1,0)、B(t,2)、C(2,1),t∈R,O为坐标原点
(I)若△ABC是∠B为直角的直角三角形,求t的值
(Ⅱ)若四边形ABCD是平行四边形,求![]() 的最小值
的最小值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com