
【题目】已知函数![]() .
.
(1)当![]() 时,函数
时,函数![]() 恰有两个不同的零点,求实数
恰有两个不同的零点,求实数![]() 的值;
的值;
(2)当![]() 时,
时,
① 若对于任意![]() ,恒有
,恒有![]() ,求
,求![]() 的取值范围;
的取值范围;
② 若![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最大值
上的最大值![]() .
.
【答案】(1) ![]() ;(2)①.
;(2)①. ![]() ;②.
;②. 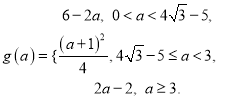
【解析】试题分析:(1)当![]() 时,考虑
时,考虑![]() 的解,化简后得到
的解,化简后得到![]() 或者
或者![]() ,它们共有两个不同的零点,所以
,它们共有两个不同的零点,所以![]() 必有解
必有解![]() ,从而
,从而![]() .
.
(2)![]() 在
在![]() 上恒成立等价于
上恒成立等价于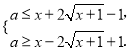 在
在![]() 上恒成立,因此考虑
上恒成立,因此考虑![]() 在
在![]() 上的最小值和
上的最小值和![]() 在
在![]() 上的最大值即可得到
上的最大值即可得到![]() 的取值范围.
的取值范围.
(3)![]() 可化为
可化为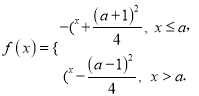 ,则当
,则当![]() 或
或![]() 时,
时, ![]() 在
在![]() 上递增;当
上递增;当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,两类情形都可以求得函数的最大值.当
上单调递减,两类情形都可以求得函数的最大值.当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,因此
上单调递增,因此![]() ,比较
,比较![]() 的大小即可得到
的大小即可得到![]() 的表达式.
的表达式.
解析:(1)当![]() 时,
时, ![]() ,由
,由![]() 解得
解得![]() 或
或![]() ,由
,由![]() 解得
解得![]() 或
或![]() .因为
.因为![]() 恰有两个不同的零点且
恰有两个不同的零点且![]() ,所以
,所以![]() ,或
,或 ![]() ,所以
,所以![]() .
.
(2)当![]() 时,
时, ![]() ,
,
①因为对于任意![]() ,恒有
,恒有![]() , 即
, 即 ![]() ,即
,即![]() ,因为
,因为![]() 时,
时, ![]() ,所以
,所以![]() , 即恒有
, 即恒有 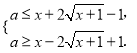 令
令![]() , 当
, 当![]() 时,
时, ![]() ,
, ![]() ,所以
,所以![]() , 所以
, 所以![]() , 所以
, 所以![]() .
.
② 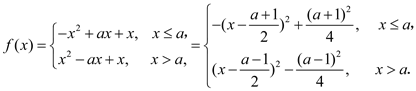
![]() 当
当![]() 时,
时, ![]() ,
,
这时![]() 在
在![]() 上单调递增,此时
上单调递增,此时![]() ;
;
![]() 当
当![]() 时,
时, ![]() ,
,
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,
, 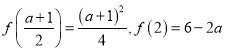 ,
,
而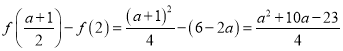
![]() ,
,
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, 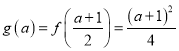 ;
;
![]() 当
当![]() 时,
时, ![]() ,
,
这时![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,此时
上单调递减,此时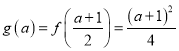 ;
;
![]() 当
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递增,此时
上单调递增,此时![]() ;
;
综上所述, ![]() 时,
时, 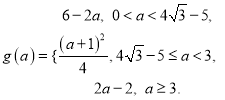


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx有两个极值点x1、x2 , 且x1<x2 , 若x1+2x0=3x2 , 函数g(x)=f(x)﹣f(x0),则g(x)( )
A.恰有一个零点
B.恰有两个零点
C.恰有三个零点
D.至多两个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和记为Sn , a1=2,an+1=Sn+2(n∈N*).
(Ⅰ)求{an}的通项公式;
(Ⅱ)求数列{nan}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)(x∈R)是偶函数,当x≥0时,f(x)=x2﹣2x.
(1)求f(x)的解析式;
(2)若不等式f(x)≥mx在1≤x≤2时都成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间的一台机床生产出一批零件,现从中抽取8件,将其编为![]() ,
, ![]() ,…,
,…, ![]() ,测量其长度(单位:
,测量其长度(单位: ![]() ),得到如表中数据:
),得到如表中数据:
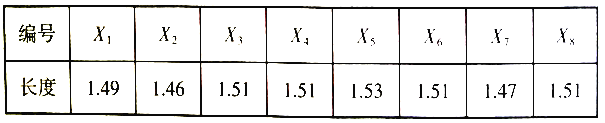
其中长度在区间![]() 内的零件为一等品.
内的零件为一等品.
(1)从上述8个零件中,随机抽取一个,求这个零件为一等品的概率;
(2)从一等品零件中,随机抽取3个.
①用零件的编号列出所有可能的抽取结果;
②求这3个零件长度相等的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com