
用向量法证明平行四边形两对角线的平方和等于四条边的平方和.
|
|
|
1.向量法解决几何问题的步骤: ①建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题; ②通过向量运算(有基向量法和坐标法两种),研究几何元素之间的关系; ③把运算结果“翻译”成几何关系. 这是用向量法解决平面几何问题的“三步曲”.又简称为:一建二算三译;也可说成为:捡便宜(建算译). 2.平面几何经常涉及距离、夹角的问题.而平面向量的运算,特别是数量积主要涉及向量的模及向量的夹角.因此,我们可以用向量方法解答几何问题.在具体问题中,先用向量表示相应的点、线段、夹角等几何元素,然后通过向量的运算,特别是数量积来研究点、线段等几何元素之间的关系,最后将结论转化为几何问题. |


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:高中数学 来源: 题型:
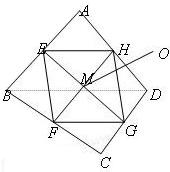 已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点.
已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点.| OM |
| 1 |
| 4 |
| OA |
| OB |
| OC |
| OD |
查看答案和解析>>
科目:高中数学 来源: 题型:
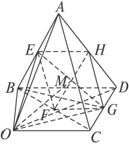
(1)用向量法证明E、F、G、H四点共面;
(2)用向量法证明BD∥平面EFGH;
(3)设M是EG和FH的交点,求证:对空间任一点O,有![]() =
=![]() (
(![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
![]() 已知E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA的中点.
已知E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA的中点.
(1)用向量法证明E、F、G、H四点共面;
(2)用向量法证明: BD∥平面EFGH;
(3)设M是EG和FH的交点,
求证:对空间任一点O,有![]() .
.
查看答案和解析>>
科目:高中数学 来源:2014届浙江省温州市高一第二学期期中考试数学试卷(解析版) 题型:解答题
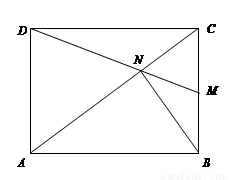
如图所示,四边形ABCD为矩形,点M是BC的中点,CN=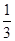 CA,用向量法证明:
CA,用向量法证明:
(1)D、N、M三点共线;(2)若四边形ABCD为正方形,则DN=BN.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com