
(本题满分12分,第1小题6分,第2小题6分)
已知集合A={x| | x–a | < 2,xÎR },B={x| <1,xÎR }.
<1,xÎR }.
(1) 求A、B;
(2) 若 ,求实数a的取值范围.
,求实数a的取值范围.
(1)A={x| a–2<x<a+2};B={x|–2<x<3}.(2)0≤a≤1.
解析试题分析:(1) 由| x–a | < 2,得a–2<x<a+2,所以A={x| a–2<x<a+2}………………………3分
由 <1,得
<1,得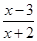 <0,即 –2<x<3,所以B={x|–2<x<3}.…………………………6分
<0,即 –2<x<3,所以B={x|–2<x<3}.…………………………6分
(2) 若AÍB,所以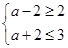 ,…………………………………………………………10分
,…………………………………………………………10分
所以0≤a≤1.………………………………………………………………………………12分
考点:含绝对值的不等式的解法;分式不等式的解法;集合间的关系。
点评:解分式不等式的主要步骤是:移项—通分—分式化整式。属于基础题型。


科目:高中数学 来源: 题型:解答题
(本题12分)已知集合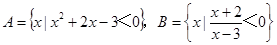
(Ⅰ)在区间(-4,4)上任取一个实数x,求“x∈A∩B”的概率;
(Ⅱ)设(a,b)为有序实数对,其中a是从集合A中任取的一个整数,b是从集合B中任取的一个整数,求“b-a∈A∪B”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com