
| A. | [$\frac{2}{3}$,$\frac{3}{2}$] | B. | [$\frac{3}{2}$,+∞) | C. | [2,3] | D. | [1,2] |
分析 将不等式进行转化,利用不等式的性质建立关于$\frac{b}{a}$的不等式关系,即可得出结论.
解答 解:∵三个正数a,b,c,满足a≤b+c≤2a,b≤a+c≤2b,
∴1≤$\frac{b}{a}$+$\frac{c}{a}$≤2①,$\frac{b}{a}$≤1+$\frac{c}{a}$≤$\frac{2b}{a}$②,
由②得-$\frac{2b}{a}$≤-1-$\frac{c}{a}$≤-$\frac{b}{a}$③,
①+③得1-$\frac{2b}{a}$≤$\frac{b}{a}$-1≤2-$\frac{b}{a}$④,
④等价于$\left\{\begin{array}{l}{1-\frac{2b}{a}≤\frac{b}{a}-1}\\{\frac{b}{a}-1≤2-\frac{b}{a}}\end{array}\right.$,
即$\left\{\begin{array}{l}{\frac{b}{a}≥\frac{2}{3}}\\{\frac{b}{a}≤\frac{3}{2}}\end{array}\right.$,
∴$\frac{2}{3}$≤$\frac{b}{a}$≤$\frac{3}{2}$.
故选:A.
点评 本题主要考查了不等式的解法与应用问题,利用不等式的性质将不等式进行转化是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
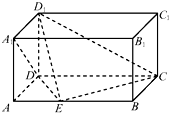 如图,已知在长方体ABCD-A1B1C1D1中,AD=A1A=$\frac{1}{2}$AB=2,点E是棱AB上一点,且$\frac{AE}{EB}$=λ.
如图,已知在长方体ABCD-A1B1C1D1中,AD=A1A=$\frac{1}{2}$AB=2,点E是棱AB上一点,且$\frac{AE}{EB}$=λ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 学生的性别与他的数学成绩 | B. | 人的工作环境与健康状况 | ||
| C. | 女儿的身高与父亲的身高 | D. | 正三角形的边长与面积 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 60°或120° | D. | 30°或150° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{4}$ | B. | 5 | C. | $\frac{{5+2\sqrt{2}}}{4}$ | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
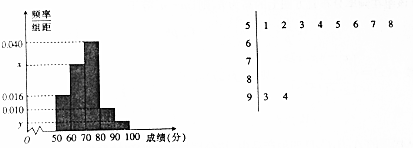
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| t(小时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1 | 0.5 | 0.99 | 1.5 |
| A. | 10小时 | B. | 8小时 | C. | 6小时 | D. | 4小时 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com