
����Ŀ��ijѧУ�о���ѧϰС��Ը�У����ѧ������������е��飬�ڸ�����ȫ��![]() ��ѧ���������ȡ��
��ѧ���������ȡ��![]() ��ѧ�������������õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ��
��ѧ�������������õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ��
�꼶���� �Ƿ���� |
|
|
���� |
|
|
������ |
|
|
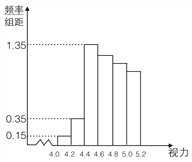
��1����ֱ��ͼ�к������Ƶ���ɵȲ����У��Թ���ȫ�꼶������![]() ���µ�������
���µ�������
��2��ѧϰС���Ա���֣�ѧϰ�ɼ�ͻ����ѧ�������ӵıȽ϶࣬Ϊ���о�ѧ����������ѧϰ�ɼ��Ƿ��й�ϵ�����꼶������![]() ����
����![]() ����ѧ�������˵��飬�õ��ұ������ݣ����ݱ��е����ݣ��ܷ��ڷ����ĸ��ʲ�����
����ѧ�������˵��飬�õ��ұ������ݣ����ݱ��е����ݣ��ܷ��ڷ����ĸ��ʲ�����![]() ��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ?
��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ?
��3���ڣ����е����![]() ��ѧ���У����շֲ�����ڲ����ӵ�ѧ���г�ȡ��
��ѧ���У����շֲ�����ڲ����ӵ�ѧ���г�ȡ��![]() �ˣ���һ�������������õĻ���ϰ�ߣ���������
�ˣ���һ�������������õĻ���ϰ�ߣ���������![]() ������ȡ
������ȡ![]() �ˣ���������
�ˣ���������![]() ��ѧ������Ϊ
��ѧ������Ϊ![]() ����
����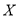 �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
|
|
|
|
|
|
|
|
|
|
| 7.879 |
![]()
���� 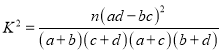
���𰸡�(1)820��(2) �ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ��(3)�𰸼�����.
��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ��(3)�𰸼�����.
�����������������(1)����ֱ��ͼ�е�ǰ�������ݺ͵Ȳ����еõ��������Ƶ�����ٹ�����Ƶ�ʺ�������(2)������![]() ��ʽ������⣬�������ٽ�ֵ�����������(3)д��������������п���ȡֵ�����ó����ηֲ��ĸ��ʹ�ʽ�����Ӧ�ĸ��ʣ����б��õ��ֲ��У����������ѧ���� .
��ʽ������⣬�������ٽ�ֵ�����������(3)д��������������п���ȡֵ�����ó����ηֲ��ĸ��ʹ�ʽ�����Ӧ�ĸ��ʣ����б��õ��ֲ��У����������ѧ���� .
�����������1����ֱ��ͼ��֪����һ����3�ˣ��ڶ�����7�ˣ���������27�ˣ�
����Ϊ�������Ƶ���ɵȲ����У����Ժ������Ƶ������Ϊ27,24,21,18����������
��![]() ���µ�Ƶ��Ϊ
���µ�Ƶ��Ϊ![]() ����ȫ�꼶������
����ȫ�꼶������![]() ���µ�����ԼΪ
���µ�����ԼΪ![]() ��
��
��2��![]() ��
��
����ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ��
��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ��
��3��������9�����꼶������![]() ����
����![]() ���ֱ���3�˺�6�ˣ�
���ֱ���3�˺�6�ˣ�
![]() ��ȡ0��1��2��3
��ȡ0��1��2��3
�� ![]() ��
�� ![]() ��
��
�� ![]() ��
�� ![]()
�� ![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() ����ѧ����
����ѧ����![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
![]() ����
����![]() ��ͼ����
��ͼ����![]() ��������
��������![]() ����
����![]() �����������������
�����������������
A. ��![]() �� B. ��
�� B. ��![]() �� C. ��
�� C. ��![]() �� D. ��
�� D. ��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ֱ���ֲ�˼�������ˮ����Ϊ���о�������ˮ���IJ���������˼ס�������ˮ���Ĺ����1000�꣮��ͳ�ƣ��õ�ÿ������������Ƶ�ʷֲ�ֱ��ͼ��ͼ��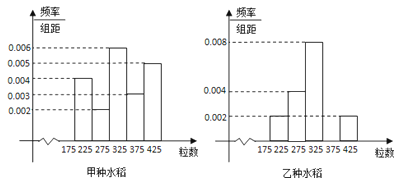
����������ˮ���������������[325��375��֮���Ƶ�ʣ�����Ƶ�ʷֲ�ֱ��ͼ���룻
�����Ը���Ƶ�ʷֲ�ֱ��ͼ���Ƽ���ˮ��������������λ����ƽ��������ȷ��0.1����
������Ƶ�ʷֲ�ֱ��ͼ�������ٴ�������Լ�������ˮ������������������ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ln��x+ ![]() ����
����
��1���жϲ�֤������y=f��x������ż�ԣ�
��2���жϲ�֤������y=f��x����R�ϵĵ����ԣ�
��3����x��[1��2]ʱ������ʽf��a4x��+f��2x+1����0���������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ƽ����һ����![]() ��������
��������![]() ��
��![]() ���ߵ�б��֮������
���ߵ�б��֮������![]() .
.
������![]() �Ĺ켣
�Ĺ켣![]() �ķ��̣�
�ķ��̣�
������ֱ��![]() ��
�� ![]() ��
��![]() ����켣
����켣![]() ����
����![]() ��
��![]() ���㣬�߶�
���㣬�߶�![]() �Ĵ�ֱƽ���߽�
�Ĵ�ֱƽ���߽�![]() ���ڵ�
���ڵ�![]() ����
����![]() �仯ʱ����
�仯ʱ����![]() ��������ֵ.
��������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������x�������ϣ�����Ϊ����ϵԭ��������߹���A��1����2����
��1���������ߵı����̣�
��2���������ߵĽ���F��ֱ��l�������߽�������M��N���ҡ�MNO��OΪԭ�㣩�����Ϊ2 ![]() ����ֱ��l�ķ��̣�
����ֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() Ϊ��Ȼ�����ĵ���.
Ϊ��Ȼ�����ĵ���.
��1������![]() ��ͼ���ܷ���
��ͼ���ܷ���![]() �����У�������
�����У�������![]() �����У���ʵ��
�����У���ʵ��![]() ��ֵ��������˵�����ɣ�
��ֵ��������˵�����ɣ�
��2��������![]() ��
��![]() �ϵ�����������ʵ��
�ϵ�����������ʵ��![]() ��ȡ�����������ֵ.
��ȡ�����������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽��һ��ĩ��ѧ���Ե�������Ӹ�һ������ѧ����ѧ�Ծ��������ȡn���Ծ����гɼ��������õ���ѧ�ɼ�Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ�������гɼ���[50��60����ѧ������Ϊ6��
������ֱ��ͼ��x��ֵ��
�����Թ�������ȡ����ѧ�ɼ���ƽ������
�����Ը����������ơ���У��һѧ����ĩ��ѧ���Գɼ���70���ĸ��ʣ�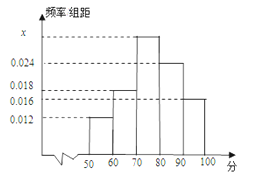
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�һ�깺��ij�ֻ���900�֣�ÿ�ζ�����x�֣��˷�Ϊÿ��9��Ԫ��һ����ܴ洢����Ϊ9x��Ԫ��
��1��Ҫʹһ������˷����ܴ洢����֮����С����ÿ�ι�����ٶ֣�
��2��Ҫʹһ������˷����ܴ洢����֮�Ͳ�����585��Ԫ����ÿ�ι�������ʲô��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com