Question

2．已知点P，Q为圆C：x²+y²=25上的任意两点，且|PQ|＜6，若PQ中点组成的区域为M，在圆C内任取一点，则该点落在区域M上的概率为$\frac{9}{25}$．

Answer 1

分析 根据直线和圆的位置关系求出平面区域M的图形，利用几何概型的概率公式即可得到结论．

解答 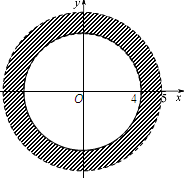解：当|PQ|=6时，圆心到线段PQ的距离d=$\sqrt{{5}^{2}-{3}^{2}}$=4．
此时M位于半径是4的圆上，
∴|PQ|＜6，
∴PQ中点组成的区域为M为半径为4的圆与半径为5的圆组成的圆环，即16＜x²+y²＜25，
PQ中点组成的区域为M如图所示，
那么在C内部任取一点落在M内的概率为$\frac{25π-16π}{25π}$=$\frac{9}{25}$，
故答案为：$\frac{9}{25}$．

点评 本题主要考查几何概型的概率计算，根据条件求出相应的区域及其面积是解决本题的关键．