
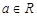 ,函数
,函数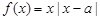 .
.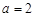 时,写出函数
时,写出函数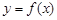 的单调递增区间;
的单调递增区间;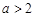 时,求函数
时,求函数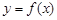 在区间[1,2]上的最小值;
在区间[1,2]上的最小值;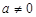 ,函数
,函数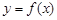 在(m,n)上既有最大值又有最小值,请分别求出m,n的取值范围(用a表示).
在(m,n)上既有最大值又有最小值,请分别求出m,n的取值范围(用a表示).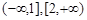 ;(2)
;(2)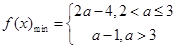 ;(3)详见解析.
;(3)详见解析.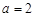 时,函数去掉绝对值后可发现它的图象是由两段抛物线的各自一部分组成,画出其图象,容易判断函数
时,函数去掉绝对值后可发现它的图象是由两段抛物线的各自一部分组成,画出其图象,容易判断函数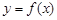 的单调递增区间;(2)
的单调递增区间;(2)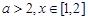 时,所以
时,所以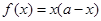 ,这是二次函数,求其在闭区间上
,这是二次函数,求其在闭区间上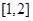 的最小值,一般要分类讨论,考虑对称轴和区间的相对位置关系,从而判断其单调性,从而求出最小值;(3)函数在开区间上有最大值和最小值,必然要使开区间上有极大值和极小值,且使极值为最值,由于函数是与二次函数相关,可考虑用数形结合的方法解答.
的最小值,一般要分类讨论,考虑对称轴和区间的相对位置关系,从而判断其单调性,从而求出最小值;(3)函数在开区间上有最大值和最小值,必然要使开区间上有极大值和极小值,且使极值为最值,由于函数是与二次函数相关,可考虑用数形结合的方法解答.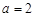 时,
时,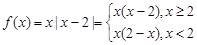 , 2分
, 2分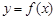 的单调递增区间为
的单调递增区间为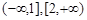 . 4分
. 4分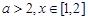 ,所以
,所以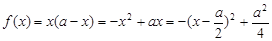 . 6分
. 6分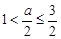 ,即
,即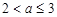 时,
时,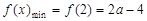 ; 7分
; 7分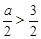 ,即
,即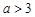 时,
时,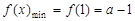 . 8分
. 8分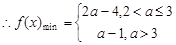 . 9分
. 9分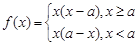 , 10分
, 10分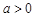 时,图象如图1所示.
时,图象如图1所示.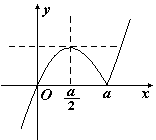
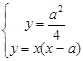 得
得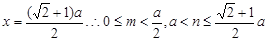 . 12分
. 12分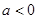 时,图象如图2所示.
时,图象如图2所示.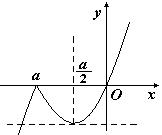
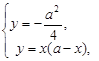 得
得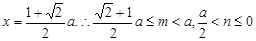 . 14分
. 14分

 口算能手系列答案
口算能手系列答案科目:高中数学 来源:不详 题型:解答题
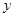 (单位:千套)与销售价格
(单位:千套)与销售价格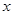 (单位:元/套)满足的关系式
(单位:元/套)满足的关系式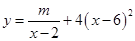 ,其中
,其中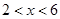 ,
,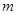 为常数.已知销售价格为4元/套时,每日可售出套题21千套.
为常数.已知销售价格为4元/套时,每日可售出套题21千套.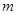 的值;
的值;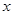 的值,使网校每日销售套题所获得的利润最大.(保留1位小数点)
的值,使网校每日销售套题所获得的利润最大.(保留1位小数点)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
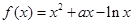 ,
,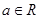 ;
;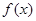 在[1,2]上是减函数,求实数
在[1,2]上是减函数,求实数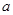 的取值范围;
的取值范围; ,是否存在实数
,是否存在实数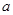 ,当
,当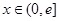 (
(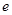 是自然对数的底数)时,函数
是自然对数的底数)时,函数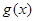 的最小值是
的最小值是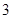 .若存在,求出
.若存在,求出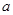 的值;若不存在,说明理由.
的值;若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 .若乙方每生产一吨产品必须赔付甲方S元(以下称S为赔付价格).
.若乙方每生产一吨产品必须赔付甲方S元(以下称S为赔付价格).查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
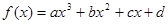
 ,给出定义:
,给出定义: 是函数
是函数 的导函数,
的导函数, 是
是 的导函数,若方程
的导函数,若方程 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 的“拐点”.某同学经研究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且拐点就是对称中心.若
的“拐点”.某同学经研究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且拐点就是对称中心.若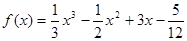 ,请你根据这一发现,求:(1)函数
,请你根据这一发现,求:(1)函数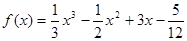 的对称中心为__________;(2)
的对称中心为__________;(2)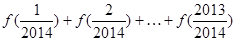 =________.
=________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com