
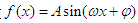 (其中
(其中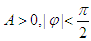 )的图象如图所示,把函数
)的图象如图所示,把函数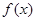 的图像向右平移
的图像向右平移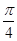 个单位,再向下平移1个单位,得到函数
个单位,再向下平移1个单位,得到函数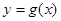 的图像.
的图像.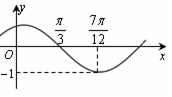
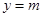 与函数
与函数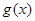 图像在
图像在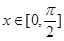 时有两个公共点,其横坐标分别为
时有两个公共点,其横坐标分别为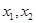 ,求
,求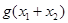 的值;
的值;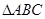 内角
内角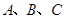 的对边分别为
的对边分别为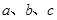 ,且
,且
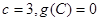 .若向量
.若向量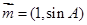 与
与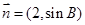 共线,求
共线,求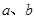 的值.
的值.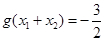 ;(2)
;(2)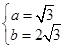
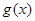 的解析式,由于
的解析式,由于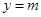 与
与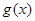 在
在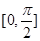 上有2个公共点,根据函数图像的对称性得到2个交点的横坐标的中点为
上有2个公共点,根据函数图像的对称性得到2个交点的横坐标的中点为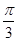 ,所以
,所以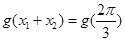 得出函数值;第二问,先用
得出函数值;第二问,先用 在
在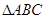 中解出角
中解出角 的值,再利用两向量共线的充要条件得到
的值,再利用两向量共线的充要条件得到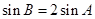 ,从而利用正弦定理得出
,从而利用正弦定理得出 ,最后利用余弦定理列出方程解出边
,最后利用余弦定理列出方程解出边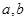 的长.
的长.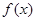 的图象,
的图象, ,得
,得 ,
,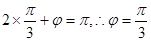 ,所以
,所以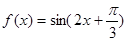 2分
2分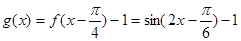 4分
4分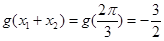 6分
6分 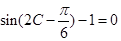 , 即
, 即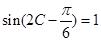
 ,
,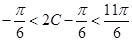 ,
, ,∴
,∴ 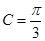 . 7分
. 7分 共线,∴
共线,∴ 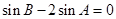 .
. , 得
, 得 ① 9分
① 9分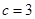 ,由余弦定理,得
,由余弦定理,得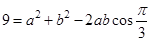 , ② 11分
, ② 11分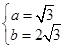 . 12分
. 12分

科目:高中数学 来源:不详 题型:单选题
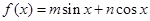 ,且
,且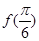 是它的最大值,(其中m、n为常数且
是它的最大值,(其中m、n为常数且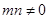 )给出下列命题:①
)给出下列命题:①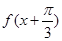 是偶函数;②函数
是偶函数;②函数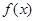 的图象关于点
的图象关于点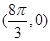 对称;③
对称;③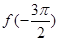 是函数
是函数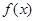 的最小值;④
的最小值;④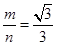 .
.| A.①②③④ | B.②③ | C.①②④ | D.②④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 sin x,sin x),b=(cos x,sin x),x∈
sin x,sin x),b=(cos x,sin x),x∈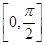 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com