
古希腊著名的毕达哥拉斯学派把1、3、6、10 这样的数称为“三角形数”,而把1、4、9、16 这样的数称为“正方形数”.如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和,下列等式中,符合这一规律的表达式是
①13=3+10; ②25=9+16 ③36=15+21; ④49=18+31;⑤64=28+36
③⑤
解析试题分析:题目中“三角形数”的规律为1、3、6、10、15、21…“正方形数”的规律为1、4、9、16、25…,根据题目已知条件:从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.可得出最后结果.解:这些三角形数的规律是1,3,6,10,15,21,28,36,45,…,且正方形数是这串数中相邻两数之和,很容易看到:恰有15+21=36.和64=28+36故答案为③⑤
考点:归纳推理
点评:本题考查探究、归纳的数学思想方法.本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:填空题
所有真约数(除本身之外的正约数)的和等于它本身的正整数叫做完全数.
如: ;
; ;
; .
.
已经证明:若 是质数,则
是质数,则 是完全数,
是完全数,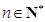 .请写出一个四位完全数 ;又
.请写出一个四位完全数 ;又 ,所以
,所以 的所有正约数之和可表示为
的所有正约数之和可表示为 ;
; ,所以
,所以 的所有正约数之和可表示为
的所有正约数之和可表示为 ;
;
按此规律, 的所有正约数之和可表示为 .
的所有正约数之和可表示为 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
平面上有 条直线, 这
条直线, 这 条直线任意两条不平行, 任意三条不共点, 记这
条直线任意两条不平行, 任意三条不共点, 记这 条直线将平面分成
条直线将平面分成 部分, 则
部分, 则 ___________,
___________,  时,
时, _________________.)(用
_________________.)(用 表示).
表示).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
观察下列算式:
13 =1,
23 =3+5,
33 = 7+9+11
43 ="13" +15 +17 +19 ,
… …
若某数n3按上述规律展开后,发现等式右边含有“2013”这个数,则n= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com