
分析 (1)求出函数的导数,根据f′(1)=2e-2,求出a的值即可;
(2)求出函数f(x)的导数,解关于导函数的不等式,求出函数的单调区间,得到关于m的不等式组,解出即可.
解答 解:(1)由f(x)=x(ex-1)-ax2得f′(x)=ex-1+xex-2ax,…(2分)
则f′(1)=2e-1-2a,由导数的几何意义得2e-1-2a=2e-2,解得$a=\frac{1}{2}$. …(5分)
(2)由(1)得$f(x)=x({e^x}-1)-\frac{1}{2}{x^2}$
则f′(x)=ex-1+xex-x=(x+1)(ex-1)…(7分)
由f′(x)=0得x=-1或x=0;由f′(x)>0得x<-1或x>0;由f′(x)<0得-1<x<0,列表如下:
| x | x<-1 | x=-1 | -1<x<0 | x=0 | x>0 |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 增 | 极大 | 减 | 极小 | 增 |
点评 本题考查了函数的单调性问题,考查导数的应用以及切线的意义,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,O是坐标原点,两个正方形OABC、BDEF的顶点中,O、A、C、D、F五个点都在抛物线y2=2px(p>0)上,另外,B、E两个点都在x轴上,若这两个正方形的面积之和为10,则( )
如图所示,O是坐标原点,两个正方形OABC、BDEF的顶点中,O、A、C、D、F五个点都在抛物线y2=2px(p>0)上,另外,B、E两个点都在x轴上,若这两个正方形的面积之和为10,则( )| A. | p=1 | B. | p=2 | C. | p=$\frac{1}{2}$ | D. | p=$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{10}}}{10}$ | B. | $\frac{{\sqrt{10}}}{10}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{{\sqrt{15}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
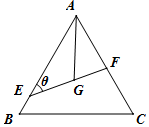 如图所示,△ABC是边长为6的等边三角形,G是它的重心(三条中线的交点),过G的直线分别交线段AB、AC于E、F两点,∠AEG=θ.
如图所示,△ABC是边长为6的等边三角形,G是它的重心(三条中线的交点),过G的直线分别交线段AB、AC于E、F两点,∠AEG=θ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
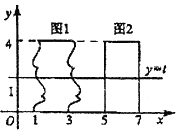 我国南北朝时代的数学家祖暅提出体积的计算原理(组暅原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是:如果两等高的几何体在同高处裁得两几何体的裁面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个矩形,且当实数t取[0,4]上的任意值时,直线y=t被图1和图2所截得的线段始终相等,则图1的面积为8.
我国南北朝时代的数学家祖暅提出体积的计算原理(组暅原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是:如果两等高的几何体在同高处裁得两几何体的裁面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个矩形,且当实数t取[0,4]上的任意值时,直线y=t被图1和图2所截得的线段始终相等,则图1的面积为8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com