
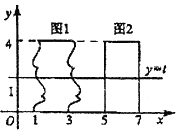
 �ҹ��ϱ���ʱ������ѧ���敜�������ļ���ԭ�����镜ԭ�����������Ƽ�ͬ����������족�����ơ����Ǹߣ����ݡ����������˼�ǣ�������ȸߵļ�������ͬ�ߴ��õ���������IJ������ȣ���ô������������������ȣ�����敜ԭ������ͼ��ʾ����ƽ��ֱ������ϵ�У�ͼ1��һ����״������ķ��ͼ�Σ�ͼ2��һ�����Σ��ҵ�ʵ��tȡ[0��4]�ϵ�����ֵʱ��ֱ��y=t��ͼ1��ͼ2���صõ��߶�ʼ����ȣ���ͼ1�����Ϊ8��
�ҹ��ϱ���ʱ������ѧ���敜�������ļ���ԭ�����镜ԭ�����������Ƽ�ͬ����������족�����ơ����Ǹߣ����ݡ����������˼�ǣ�������ȸߵļ�������ͬ�ߴ��õ���������IJ������ȣ���ô������������������ȣ�����敜ԭ������ͼ��ʾ����ƽ��ֱ������ϵ�У�ͼ1��һ����״������ķ��ͼ�Σ�ͼ2��һ�����Σ��ҵ�ʵ��tȡ[0��4]�ϵ�����ֵʱ��ֱ��y=t��ͼ1��ͼ2���صõ��߶�ʼ����ȣ���ͼ1�����Ϊ8�� 
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��c��b | B�� | b��c��a | C�� | c��b��a | D�� | c��a��b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-2��1�� | B�� | ��1��2] | C�� | [-2��-1�� | D�� | ��-1��2] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������PDC���ڵ�ƽ���볤����ABCD���ڵ�ƽ�洹ֱ��
��ͼ��������PDC���ڵ�ƽ���볤����ABCD���ڵ�ƽ�洹ֱ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x3•x2=x5 | B�� | x+x2=x3 | C�� | 2x3��x2=x | D�� | ��$\frac{x}{2}$��3=$\frac{{x}^{3}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| 16 | 22 | 77 | 94 | 39 | 49 | 54 | 43 | 54 | 82 | 17 | 37 | 93 | 23 | 78 | 87 | 35 | 20 | 96 | 43 |
| 84 | 42 | 17 | 53 | 31 | 57 | 24 | 55 | 06 | 88 | 77 | 04 | 74 | 47 | 67 | 21 | 76 | 33 | 50 | 25 |
| A�� | 23 | B�� | 37 | C�� | 35 | D�� | 17 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��$\frac{\sqrt{7}}{3}$] | B�� | ��0��$\frac{\sqrt{5}}{2}$] | C�� | ��$\sqrt{2}$��$\frac{5}{3}$] | D�� | ��$\sqrt{2}$��$\frac{\sqrt{13}}{3}$] |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com