
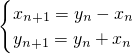 (n∈N*)为点Pn(xn,yn)到点Pn+1(xn+1,yn+1)的一个变换,我们把它称为点变换.已知P1(0,1),P2(x2,y2),…,Pn(xn,yn),Pn+1(xn+1,yn+1)(n∈N*)是经过点变换得到的一列点.设an=|PnPn+1|,数列{an}的前n项和为Sn,那么S20的值为
(n∈N*)为点Pn(xn,yn)到点Pn+1(xn+1,yn+1)的一个变换,我们把它称为点变换.已知P1(0,1),P2(x2,y2),…,Pn(xn,yn),Pn+1(xn+1,yn+1)(n∈N*)是经过点变换得到的一列点.设an=|PnPn+1|,数列{an}的前n项和为Sn,那么S20的值为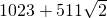
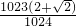
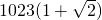
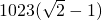
 ,a3=|p3P4|=2,a4=|p4P5|=
,a3=|p3P4|=2,a4=|p4P5|= ,…an=
,…an= n-1,Sn=a1+a2+a3+…+an=
n-1,Sn=a1+a2+a3+…+an=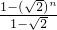 ,∴故可求S20的值
,∴故可求S20的值 ,a3=|p3P4|=2,a4=|p4P5|=
,a3=|p3P4|=2,a4=|p4P5|= ,…an=
,…an= n-1,
n-1,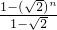 ,∴S20=
,∴S20=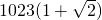 ,
,

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:高中数学 来源: 题型:
|
|
|
|
| π |
| 3 |
| 5 |
| 1 |
| a |
| 4 |
| b |
| 9 |
| a+b |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 |
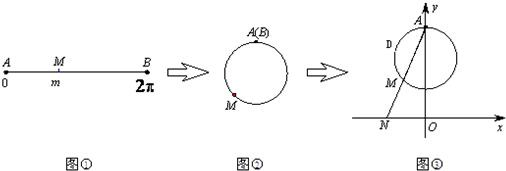
| ADM |
| π |
| 2 |
| 5π |
| 3 |
| π |
| 4 |
| 5π |
| 6 |
| π |
| 4 |
| 5π |
| 6 |
查看答案和解析>>
科目:高中数学 来源:2010年上海市闵行区高考数学一模试卷(文科)(解析版) 题型:选择题
 (n∈N*)为点Pn(xn,yn)到点Pn+1(xn+1,yn+1)的一个变换,我们把它称为点变换.已知P1(0,1),P2(x2,y2),…,Pn(xn,yn),Pn+1(xn+1,yn+1)(n∈N*)是经过点变换得到的一列点.设an=|PnPn+1|,数列{an}的前n项和为Sn,那么S20的值为( )
(n∈N*)为点Pn(xn,yn)到点Pn+1(xn+1,yn+1)的一个变换,我们把它称为点变换.已知P1(0,1),P2(x2,y2),…,Pn(xn,yn),Pn+1(xn+1,yn+1)(n∈N*)是经过点变换得到的一列点.设an=|PnPn+1|,数列{an}的前n项和为Sn,那么S20的值为( )



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com