
【题目】三棱柱ABC﹣A1B1C1中,平面AA1B1B⊥平面ABC,AB=AA1=A1B=4,BC=2,AC=2![]() ,点F为AB的中点,点E为线段A1C1上的动点.
,点F为AB的中点,点E为线段A1C1上的动点.
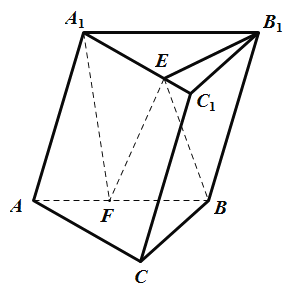
(1)求证:BC⊥平面A1EF;
(2)若∠B1EC1=60°,求四面体A1B1EF的体积.
【答案】(1)证明见解析.(2)![]()
【解析】
(1)利用等边三角形的性质可得:A1F⊥AB.利用线面、面面垂直的判定定理与性质定理可得:A1F⊥BC.利用勾股定理的逆定理可得:BC⊥AC.进而证明结论.
(2)利用直角三角形的边角关系可得:EC1![]() ,A1E.由(I)可得:A1F⊥底面A1B1C1,A1F⊥A1E,A1F=2
,A1E.由(I)可得:A1F⊥底面A1B1C1,A1F⊥A1E,A1F=2![]() .可得△A1EF的面积S.由(I)可得:BC⊥平面A1EF,可得B1C1⊥平面A1EF,即可得出四面体A1B1EF的体积.
.可得△A1EF的面积S.由(I)可得:BC⊥平面A1EF,可得B1C1⊥平面A1EF,即可得出四面体A1B1EF的体积.
(1)∵AB=AA1=A1B,点F为AB的中点,∴A1F⊥AB,
∵平面AA1B1B⊥平面ABC,平面AA1B1B∩平面ABC=AB,
∴A1F⊥平面ABC,BC平面ABC,∴A1F⊥BC.
∵AB=4,BC=2,AC=2![]() ,∴AB2=BC2+AC2,∴∠ACB=90°,∴BC⊥AC.
,∴AB2=BC2+AC2,∴∠ACB=90°,∴BC⊥AC.
∵AC∥A1C1,∴BC⊥A1C1,又A1F∩A1E=A1,∴BC⊥平面A1EF;
(2)∵∠B1EC1=60°,∴EC1![]() ,∴A1E=2
,∴A1E=2![]() .
.
由(1)可得:A1F⊥底面A1B1C1,∴A1F⊥A1E,A1F=2![]() .
.
∴△A1EF的面积S![]() 4.
4.
由(1)可得:BC⊥平面A1EF,∵B1C1∥BC,∴B1C1⊥平面A1EF,
∴四面体A1B1EF的体积![]() SB1C1
SB1C1![]() 4×2
4×2![]() .
.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线C1:x2=2py(p>0),圆C2:x2+y2﹣8y+12=0的圆心M到抛物线C1的准线的距离为![]() ,点P是抛物线C1上一点,过点P,M的直线交抛物线C1于另一点Q,且|PM|=2|MQ|,过点P作圆C2的两条切线,切点为A、B.
,点P是抛物线C1上一点,过点P,M的直线交抛物线C1于另一点Q,且|PM|=2|MQ|,过点P作圆C2的两条切线,切点为A、B.
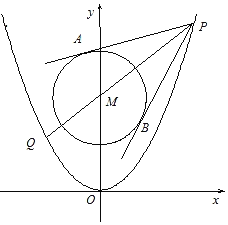
(Ⅰ)求抛物线C1的方程;
(Ⅱ)求直线PQ的方程及![]()
![]()
![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】纸张的规格是指纸张制成后,经过修整切边,裁成一定的尺寸.现在我国采用国际标准,规定以![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 等标记来表示纸张的幅面规格.复印纸幅面规格只采用
等标记来表示纸张的幅面规格.复印纸幅面规格只采用![]() 系列和
系列和![]() 系列,其中系列的幅面规格为:①
系列,其中系列的幅面规格为:①![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 所有规格的纸张的幅宽(以
所有规格的纸张的幅宽(以![]() 表示)和长度(以
表示)和长度(以![]() 表示)的比例关系都为
表示)的比例关系都为![]() ;②将
;②将![]() 纸张沿长度方向对开成两等分,便成为
纸张沿长度方向对开成两等分,便成为![]() 规格,
规格,![]() 纸张沿长度方向对开成两等分,便成为
纸张沿长度方向对开成两等分,便成为![]() 规格,…,如此对开至
规格,…,如此对开至![]() 规格.现有
规格.现有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 纸各一张.若
纸各一张.若![]() 纸的宽度为
纸的宽度为![]() ,则
,则![]() 纸的面积为________
纸的面积为________![]() ;这
;这![]() 张纸的面积之和等于________
张纸的面积之和等于________![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
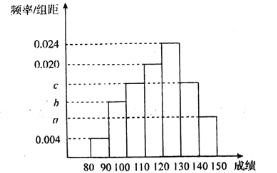
【题目】高三年级某班50名学生期中考试数学成绩的频率分布直方图如图所示,成绩分组区间为:![]()
![]()
![]()
![]()
![]()
![]()
![]() .其中a,b,c成等差数列且
.其中a,b,c成等差数列且![]() .物理成绩统计如表.(说明:数学满分150分,物理满分100分)
.物理成绩统计如表.(说明:数学满分150分,物理满分100分)
分组 |
|
|
|
|
|
频数 | 6 | 9 | 20 | 10 | 5 |
(1)根据频率分布直方图,请估计数学成绩的平均分;
(2)根据物理成绩统计表,请估计物理成绩的中位数;
(3)若数学成绩不低于140分的为“优”,物理成绩不低于90分的为“优”,已知本班中至少有一个“优”同学总数为6人,从此6人中随机抽取3人,记X为抽到两个“优”的学生人数,求X的分布列和期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机运动计步已成为一种时尚,某中学统计了该校教职工一天行走步数(单位:百步),绘制出如下频率分布直方图:
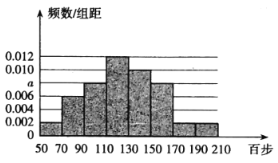
(Ⅰ)求直方图中![]() 的值,并由频率分布直方图估计该校教职工一天步行数的中位数;
的值,并由频率分布直方图估计该校教职工一天步行数的中位数;
(Ⅱ)若该校有教职工175人,试估计一天行走步数不大于130百步的人数;
(Ⅲ)在(Ⅱ)的条件下该校从行走步数大于150百步的3组教职工中用分层抽样的方法选取6人参加远足活动,再从6人中选取2人担任领队,求这两人均来自区间![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是椭圆
是椭圆![]() 的左右焦点,椭圆与
的左右焦点,椭圆与![]() 轴正半轴交于点
轴正半轴交于点![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,且
,且![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)![]() 为椭圆
为椭圆![]() 上任意一点,过
上任意一点,过![]() ,
,![]() 分别作直线
分别作直线![]() ,
,![]() ,且
,且![]() 与
与![]() 相交于
相交于![]() 轴上方一点
轴上方一点![]() ,当
,当![]() 时,求
时,求![]() ,
,![]() 两点间距离的最大值.
两点间距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx-a![]() .
.
(1)若a=-1,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若f(x)![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,菱形ABCD与正三角形BCE的边长均为2,它们所在的平面互相垂直,DF⊥平面ABCD且DF![]() .
.
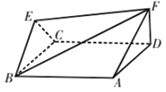
(1)求证:EF//平面ABCD;
(2)若∠ABC=∠BCE,求二面角A﹣BF﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最大值为
的最大值为![]() ,其图象相邻两条对称轴之间的距离为
,其图象相邻两条对称轴之间的距离为![]() ,且
,且![]() 的图象关于点
的图象关于点![]() 对称,则下列判断正确的是( )
对称,则下列判断正确的是( )
A.要得到函数![]() 的图象,只需将
的图象,只需将![]() 向右平移
向右平移![]() 个单位
个单位
B.函数![]() 的图象关于直线
的图象关于直线![]() 对称
对称
C.当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]()
D.函数![]() 在
在![]() 上单调递增
上单调递增
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com