
【题目】如图所示,菱形ABCD与正三角形BCE的边长均为2,它们所在的平面互相垂直,DF⊥平面ABCD且DF![]() .
.
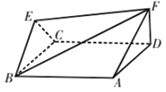
(1)求证:EF//平面ABCD;
(2)若∠ABC=∠BCE,求二面角A﹣BF﹣E的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)要线面平行,即证直线在面外且直线平行于平面内的一条直线,故过点E作EH⊥BC于![]() 构造平行四边形即可得到线线平行.
构造平行四边形即可得到线线平行.
(2)连接HA,根据题意,AH⊥BC,以H为原点,HB,HA,HE为x,y,z轴建立空间直角坐标系,分别求出平面BAF和平面BEF的法向量,利用法向量求出二面角的余弦值.
(1)过点E作EH⊥BC,连接HD,EH![]() ,
,
因为平面ABCD⊥平面BCE,EH平面BCE,
平面ABCD∩平面BCE=BC,
所以EH⊥平面ABCD,
因为FD⊥ABCD,FD![]() ,
,
所以FD//EH,FD=EH,故平行四边形EHDF,
所以EF//HD,
由EF平面ABCD,HD平面ABCD,
所以EF//平面ABCD;
(2)连接HA,根据题意,AH⊥BC,
如图:
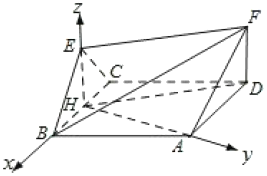
以H为原点,HB,HA,HE为x,y,z轴建立空间直角坐标系,
则A(0,![]() ,0),B(1,0,0),E(0,
,0),B(1,0,0),E(0,![]() ,
,![]() ),F(-2,
),F(-2,![]() ,
,![]() ),
),
则![]() (﹣1,
(﹣1,![]() ,0),
,0),![]() (﹣1,0,
(﹣1,0,![]() ),
),![]() (﹣3,
(﹣3,![]() ,
,![]() ),
),
设平面BAF的法向量为![]() (x,y,z),
(x,y,z),
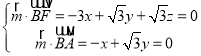 ,得
,得![]() (
(![]() ,1,2),
,1,2),
设平面BEF的法向量为![]() ,
,
由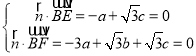 ,得
,得![]() ,
,
由cos![]() ,
,
所以二面角A﹣FB﹣E的余弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】三棱柱ABC﹣A1B1C1中,平面AA1B1B⊥平面ABC,AB=AA1=A1B=4,BC=2,AC=2![]() ,点F为AB的中点,点E为线段A1C1上的动点.
,点F为AB的中点,点E为线段A1C1上的动点.
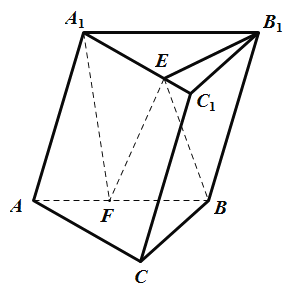
(1)求证:BC⊥平面A1EF;
(2)若∠B1EC1=60°,求四面体A1B1EF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,动直线l与椭圆E交于不同的两点
,动直线l与椭圆E交于不同的两点![]() ,
,![]() ,且△AOB的面积为1,其中O为坐标原点.
,且△AOB的面积为1,其中O为坐标原点.
(1)证明:![]() 为定值;
为定值;
(2)设线段AB的中点为M,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() 1(a
1(a![]() 0,b
0,b![]() 0)的左右焦点分别为F1,F2,点O为坐标原点,点P在双曲线的右支上,且满足|F1F2|=2|OP|.若直线PF2与双曲线C只有一个交点,则双曲线C的离心率为( )
0)的左右焦点分别为F1,F2,点O为坐标原点,点P在双曲线的右支上,且满足|F1F2|=2|OP|.若直线PF2与双曲线C只有一个交点,则双曲线C的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新型冠状病毒属于![]() 属的冠状病毒,有包膜,颗粒常为多形性,其中包含着结构为数学模型的
属的冠状病毒,有包膜,颗粒常为多形性,其中包含着结构为数学模型的![]() ,
,![]() ,人体肺部结构中包含
,人体肺部结构中包含![]() ,
,![]() 的结构,新型冠状病毒肺炎是由它们复合而成的,表现为
的结构,新型冠状病毒肺炎是由它们复合而成的,表现为![]() .则下列结论正确的是( )
.则下列结论正确的是( )
A.若![]() ,则
,则![]() 为周期函数
为周期函数
B.对于![]() ,
,![]() 的最小值为
的最小值为![]()
C.若![]() 在区间
在区间![]() 上是增函数,则
上是增函数,则![]()
D.若![]() ,
,![]() ,满足
,满足![]() ,则
,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ex﹣ax+a(a∈R),其图象与x轴交于A(x1,0),B(x2,0)两点,且x1<x2.
(1)求a的取值范围;
(2)证明:f′(![]() )<0(f′(x)为函数f(x)的导函数);
)<0(f′(x)为函数f(x)的导函数);
(3)设点C在函数y=f(x)的图象上,且△ABC为等腰直角三角形,记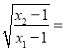 t,求(a﹣1)(t﹣1)的值.
t,求(a﹣1)(t﹣1)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别是
,左、右焦点分别是![]() ,椭圆
,椭圆![]() 上短轴的一个端点与两个焦点构成的三角形的面积为
上短轴的一个端点与两个焦点构成的三角形的面积为![]() ;
;
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(点
两点(点![]() 在第二象限),
在第二象限),![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点,若
两侧的动点,若![]() ,求证:直线
,求证:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 过点A
过点A![]() ,两个焦点为(-1,0),(1,0)。
,两个焦点为(-1,0),(1,0)。
(Ⅰ)求椭圆C的方程;
(Ⅱ)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com