
| A. | -$\frac{35}{2}$ | B. | 70 | C. | $\frac{35}{2}$ | D. | -70 |
分析 根据($\frac{1}{2}$x-2y)2n+1展开式中前n+1项的二项式系数之和等于后n+1项的和,
求出n的值,再利用展开式的通项公式求出x4y3的系数.
解答 解:($\frac{1}{2}$x-2y)2n+1展开式中共有2n+2项,
其前n+1项的二项式系数之和等于后n+1项和,
∴22n+1=64×2,解得n=3;
∴($\frac{1}{2}$x-2y)7展开式中通项公式为
Tr+1=${C}_{7}^{r}$•${(\frac{1}{2}x)}^{7-r}$•(-2y)r,
令r=3,得展开式中x4y3的系数是
${C}_{7}^{3}$•${(\frac{1}{2})}^{4}$•(-2)3=-$\frac{35}{2}$.
故选:A.
点评 本题考查了二项式展开式的通项公式与二项式系数的应用问题,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | 4(1+$\sqrt{2}$) | B. | 4+$\sqrt{2}$ | C. | 2($\sqrt{2}$+$\sqrt{6}$) | D. | $\sqrt{6}$+3$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{4}}]$ | B. | $({\frac{1}{4},\frac{1}{2}}]$ | C. | $[{\frac{1}{4},\frac{1}{2}})$ | D. | $({0,\frac{1}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
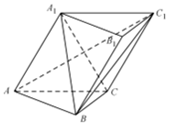 如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,底面ABC是等腰直角三角形,CA=CB,A1B⊥AC1.
如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,底面ABC是等腰直角三角形,CA=CB,A1B⊥AC1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | n<2017 | B. | n≤2017 | C. | n>2017 | D. | n≥2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}$$-\frac{{y}^{2}}{16}$=1 | B. | x2-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{2}$$-\frac{{y}^{2}}{3}$=1 | D. | x2$-\frac{{y}^{2}}{6}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1260 | B. | 1360 | C. | 1430 | D. | 1530 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com