
【题目】解下列关于x的不等式.
(1) 4x-![]() -7·2x-2-1>0;
-7·2x-2-1>0;
(2) loga(2x+1)>2loga(1-x)(其中a是正的常数,且a≠1).
【答案】(1){x|x>2}.(2)见解析
【解析】试题分析:(1)利用![]() 二次关系,将不等式转化为一元二次不等式,解得2x-4>0,再根据指数函数单调性解得x>2.(2)先根据真数大于零得-
二次关系,将不等式转化为一元二次不等式,解得2x-4>0,再根据指数函数单调性解得x>2.(2)先根据真数大于零得-![]() <x<1,再根据对数函数单调性分类讨论:若a>1,则2x+1>(1-x)2,解得0<x<4;② 若0<a<1,则2x+1<(1-x)2,x2-4x>0,解得x<0或x>4,最后综合条件得当a>1时,不等式解集是(0,1);当0<a<1时,不等式解集是(-
<x<1,再根据对数函数单调性分类讨论:若a>1,则2x+1>(1-x)2,解得0<x<4;② 若0<a<1,则2x+1<(1-x)2,x2-4x>0,解得x<0或x>4,最后综合条件得当a>1时,不等式解集是(0,1);当0<a<1时,不等式解集是(-![]() ,0).
,0).
试题解析:解:(1) 原不等式可化为2·4x-7·2x-4>0,即(2·2x+1)(2x-4)>0.
∵ 2x>0,∴ 2·2x+1>0,∴ 2x-4>0,解得x>2.
∴ 不等式的解集为{x|x>2}.
(2) 由![]() 得-
得-![]() <x<1.
<x<1.
将原不等式化为loga(2x+1)>loga(1-x)2.
① 若a>1,则2x+1>(1-x)2,x2-4x<0,解得0<x<4,又-![]() <x<1,∴ 0<x<1;
<x<1,∴ 0<x<1;
② 若0<a<1,则2x+1<(1-x)2,x2-4x>0,解得x<0或x>4,又-![]() <x<1,∴ -
<x<1,∴ -![]() <x<0.
<x<0.
综上所述,当a>1时,不等式解集是(0,1);当0<a<1时,不等式解集是(-![]() ,0).
,0).


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】某校收集该校学生从家到学校的时间后,制作成如下的频率分布直方图:
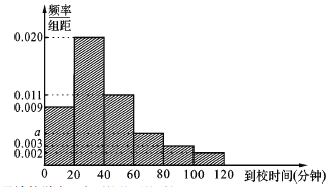
(1)求![]() 的值及该校学生从家到校的平均时间;
的值及该校学生从家到校的平均时间;
(2)若该校因学生寝室不足,只能容纳全校![]() 的学生住校,出于安全角度考虑,从家到校时间较长的学生才住校,请问从家到校时间多少分钟以上开始住校.
的学生住校,出于安全角度考虑,从家到校时间较长的学生才住校,请问从家到校时间多少分钟以上开始住校.
查看答案和解析>>
科目:高中数学 来源: 题型:
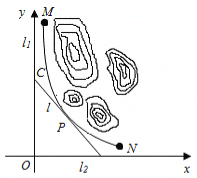
【题目】 某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路的山区边界的直线型公路,记两条相互垂直的公路为![]() ,山区边界曲线为
,山区边界曲线为![]() ,计划修建的公路为
,计划修建的公路为![]() ,如图所示,
,如图所示,![]() 为
为![]() 的两个端点,测得点
的两个端点,测得点![]() 到
到![]() 的距离分别为5千米和40千米,点
的距离分别为5千米和40千米,点![]() 到
到![]() 的距离分别为20千米和2.5千米,以
的距离分别为20千米和2.5千米,以![]() 所在的直线分别为
所在的直线分别为![]() 轴,建立平面直角坐标系
轴,建立平面直角坐标系![]() ,假设曲线
,假设曲线![]() 符合函数
符合函数![]() (其中
(其中![]() 为常数)模型.
为常数)模型.
(1)求![]() 的值;
的值;
(2)设公路![]() 与曲线
与曲线![]() 相切于
相切于![]() 点,
点,![]() 的横坐标为
的横坐标为![]() .
.
①请写出公路![]() 长度的函数解析式
长度的函数解析式![]() ,并写出其定义域;
,并写出其定义域;
②当![]() 为何值时,公路
为何值时,公路![]() 的长度最短?求出最短长度.
的长度最短?求出最短长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() .
.
(1)求函数![]() 的单调增区间;
的单调增区间;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数![]() 的图象,若
的图象,若![]() 在
在![]() 上至少含有10个零点,求
上至少含有10个零点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体![]() 中,
中,![]() ,
,![]() 是棱
是棱![]() 上的一点.
上的一点.
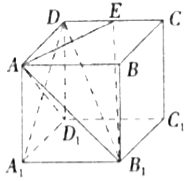
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() ;
;
(3)若![]() 是棱
是棱![]() 的中点,在棱
的中点,在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出线段
?若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(A)设函数![]() ,
, ![]() .
.
(1)证明:函数![]() 在
在![]() 上为增函数;
上为增函数;
(2)若方程![]() 有且只有两个不同的实数根,求实数
有且只有两个不同的实数根,求实数![]() 的值.
的值.
(B)已知函数![]() .
.
(1)求函数![]() 的最小值;
的最小值;
(2)若存在唯一实数![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个关于数列命题:
(1)若![]() 是等差数列,则三点
是等差数列,则三点![]() 、
、![]() 、
、![]() 共线;
共线;
(2)若![]() 是等比数列,则
是等比数列,则![]() 、
、![]() 、
、![]() (
(![]() )也是等比数列;
)也是等比数列;
(3)等比数列![]() 的前n项和为
的前n项和为![]() ,若对任意的
,若对任意的![]() ,点
,点![]() 均在函数
均在函数![]() (
(![]() ,
, ![]() 均为常数)的图象上,则r的值为
均为常数)的图象上,则r的值为![]() .
.
(4)对于数列![]() ,定义数列
,定义数列![]() 为数列
为数列![]() 的“差数列”,若
的“差数列”,若![]() ,
, ![]() 的“差数列”的通项为
的“差数列”的通项为![]() ,则数列
,则数列![]() 的前
的前![]() 项和
项和![]()
![]()
其中正确命题的个数是 ( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com