
设函数f(x)是定义在R上的偶函数,且对任意的x∈R恒有f(x+1)=f(x-1),已知当x∈[0,1]时f(x)=(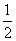 )1-x,则
)1-x,则
①2是函数f(x)的周期;
②函数f(x)在(1,2)上是减函数,在(2,3)上是增函数;
③函数f(x)的最大值是1,最小值是0;
④当x∈(3,4)时,f(x)=(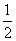 )x-3. 其中所有正确命题的序号是________.
)x-3. 其中所有正确命题的序号是________.
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
如图(1)所示,直角梯形 中,
中,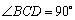 ,
,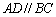 ,
, ,
,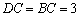 .过
.过 作
作 于
于 ,
,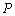 是线段
是线段 上的一个动点.将
上的一个动点.将 沿
沿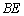 向上折起,使平面
向上折起,使平面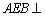 平面
平面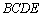 .连结
.连结 ,
, ,
, (如图(2)).
(如图(2)).
(Ⅰ)取线段 的中点
的中点 ,问:是否存在点
,问:是否存在点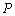 ,使得
,使得 平面
平面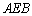 ?若存在,求出
?若存在,求出 的长;不存在,说明理由;
的长;不存在,说明理由;
 (Ⅱ)当
(Ⅱ)当 时,求平面
时,求平面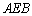 和平面
和平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
某企业2014年2月份生产A、B、C三种产品共6000件,根据分层拍样的结果,该企业统计员制作了如下的统计表格:
| 产品类别 | A | B | C |
| 产品数量 | 2600 | ||
| 样本容量 | 260 |
由于不小心,表格中B、C产品的有关数据已被污染看不清楚,统计员记得B产品的样本容量比C产品的样本容量多20,根据以上信息,可得C的产品数量是 ( )
A.160 B.180 C.1600 D.1800
查看答案和解析>>
科目:高中数学 来源: 题型:
过抛物线 y2 = 4x 的焦点作直线交抛物线于A(x1, y1)B(x2, y2)两点,如果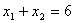
那么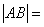 ( )
( )
A. 5 B. 6 C .7 D .8
查看答案和解析>>
科目:高中数学 来源: 题型:
某企业2012年初用72万元购进一台设备,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该设备使用后,每年的总收入为50万元,设使用 年后该设备的盈利额为
年后该设备的盈利额为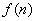 万元。(1)写出
万元。(1)写出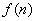 的表达式;(2)求从第几年开始,该设备开始盈利;(3)使用若干年后,对该设备的处理方案有两种:方案一:年平均盈利额达到最大值时,以48万元价格处理该设备;方案二:当盈利额达到最大值时,以16万元价格处理该设备。问用哪种方案处理较为合理?请说明理由.
的表达式;(2)求从第几年开始,该设备开始盈利;(3)使用若干年后,对该设备的处理方案有两种:方案一:年平均盈利额达到最大值时,以48万元价格处理该设备;方案二:当盈利额达到最大值时,以16万元价格处理该设备。问用哪种方案处理较为合理?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com