已知点P(3,2)及圆C:x2+y2-2x+2y-2=0.
(1)过P向圆C作切线,切点为A,B(A在B的左边),求切线的方程;
(2)求切线长|PA|,并求∠APB的正切;
(3)求直线AB的方程;
(4)求四边形ACBP的面积.
【答案】
分析:由(x-1)
2+(y+1)
2=4,可知圆心C(1,-1),半径r=2
(1)设PA的斜率为k,则PA的方程为y-2=k(x-3),由点到直线的距离公式可得

=2可求k,从而可求
(2)将x=3代入圆C可求B(3,-1),从而|PA|=|PB|=3,设PA的倾斜角为θ,则∠APB=90°-θ,由tanθ=k=

可求

(3)由

=

,及AB⊥PC可求

,从而可求直线AB的方程
(4)依据对称性可知S
ACBP=2S
△PBC=

,代入可求
解答:解:将已知圆的方程化为(x-1)
2+(y+1)
2=4,圆心C(1,-1),半径r=2(2分)(以下每题3分)
(1)设PA的斜率为k,则PA的方程为y-2=k(x-3),即kx-y-3k+2=0
由点到直线的距离公式可得,

=2
∴k=
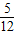
,由于过圆外一点P(3,2)作圆的切线有两条
一条切线PB的斜率不存在,从而可得两切线中,PA 的方程为5x-12y+9=0,PB的方程为x=3
∴两切线方程分别为5x-12y+9=0和x=3
(2)将x=3代入圆C::x
2+y
2-2x+2y-2=0.可得y=-1
∴B(3,-1),|PB|=3,从而|PA|=|PB|=3
又设PA的倾斜角为θ,则∠APB=90°-θ
∵tanθ=k=

∴

(3)

=

,∵AB⊥PC
∴

∵B(3,-1)
∴直线AB的方程为y+1=

(x-3)即2x+3y-3=0
(4)依据对称性可知S
ACBP=2S
△PBC=

=3×2=6
点评:此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,两点间的距离公式,,直线的倾斜角与斜率的关系点到直线的距离公式,切线的性质,勾股定理,以及直线的点斜式方程,利用了分类讨论的思想,是一道综合性较强的题.

 =2可求k,从而可求
=2可求k,从而可求 可求
可求
 =
= ,及AB⊥PC可求
,及AB⊥PC可求 ,从而可求直线AB的方程
,从而可求直线AB的方程 ,代入可求
,代入可求 =2
=2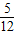 ,由于过圆外一点P(3,2)作圆的切线有两条
,由于过圆外一点P(3,2)作圆的切线有两条 ∴
∴
 =
= ,∵AB⊥PC
,∵AB⊥PC
 (x-3)即2x+3y-3=0
(x-3)即2x+3y-3=0 =3×2=6
=3×2=6

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案