
 的底面是正方形,
的底面是正方形, ,点
,点 在棱
在棱 上.
上.
 平面
平面 ;
; ,且
,且 时,确定点
时,确定点 的位置,即求出
的位置,即求出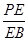 的值.
的值. 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源:不详 题型:单选题
| A.24π | B.12π | C.8π | D.4π |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
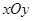 平面上,将两个半圆弧
平面上,将两个半圆弧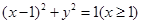 和
和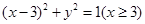 、两条直线
、两条直线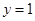 和
和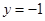 围成的封闭图形记为D,如图中阴影部分.记D绕y轴旋转一周而成的几何体为
围成的封闭图形记为D,如图中阴影部分.记D绕y轴旋转一周而成的几何体为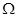 ,过
,过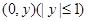 作
作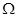 的水平截面,所得截面面积为
的水平截面,所得截面面积为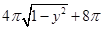 ,试利用祖暅原理、一个平放的圆柱和一个长方体,得出
,试利用祖暅原理、一个平放的圆柱和一个长方体,得出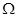 的体积值为__________
的体积值为__________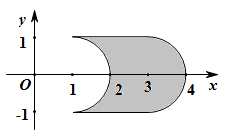
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com