
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的极值;
的极值;
(2)若对任意的![]() ,当
,当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的最大值;
的最大值;
(3)若函数![]() 恰有两个不相等的零点,求实数
恰有两个不相等的零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 的极小值为
的极小值为![]() ,无极大值;(2)
,无极大值;(2)![]() ;(3)
;(3) ![]() .
.
【解析】
(1)求出![]() ,判断其符号,得出
,判断其符号,得出![]() 的单调性即可
的单调性即可
(2)将![]() 变形为
变形为![]() ,构造函数
,构造函数![]() ,转化为
,转化为![]() 在
在![]() 恒成立即可
恒成立即可
(3)求出![]() ,然后分四种情况讨论
,然后分四种情况讨论
(1)![]() ,令
,令![]() ,得
,得![]() .
.
列表如下:
|
| 1 |
|
| - | 0 | + |
|
| 极小值 |
|
∵![]() ,∴
,∴![]() 的极小值为
的极小值为![]() ,无极大值.
,无极大值.
(2)∵![]() ,由(1)可知
,由(1)可知![]()
等价于![]() ,
,
即![]() .
.
设![]() ,则
,则![]() 在
在![]() 为增函数.
为增函数.
∴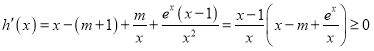 在
在![]() 恒成立.
恒成立.
∴![]() 恒成立.
恒成立.
设![]() ,∵
,∵![]() 在
在![]() 上恒成立
上恒成立
∴![]() 为增函数.
为增函数.
∴![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.
∴![]() ,∴
,∴![]() 的最大值为
的最大值为![]() .
.
(3)![]()
①当![]() 时,当
时,当![]() 和
和![]() 时,
时,![]() ,
,![]() 单调递增
单调递增
当![]() 时,
时,![]() ,
,![]() 单调递减
单调递减
所以![]() 的极大值为
的极大值为![]()
![]()
所以函数![]() 至多一个零点
至多一个零点
②当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
③当![]() 时,当
时,当![]() 和
和![]() 时,
时,![]() ,
,![]() 单调递增
单调递增
当![]() 时,
时,![]() ,
,![]() 单调递减
单调递减
所以![]() 的极大值为
的极大值为![]()
![]() 的极小值为
的极小值为![]()
所以函数![]() 至多有一个零点.
至多有一个零点.
④当![]() 时,当
时,当![]() ,
,![]() ,
,![]() 单调递增
单调递增
当![]() 时,
时,![]() ,
,![]() 单调递减
单调递减
所以![]()
Ⅰ:当![]() 时,即
时,即![]() 时,函数
时,函数![]() 至多一个零点.
至多一个零点.
Ⅱ:当![]() 时,
时,![]()
所以存在![]() ,
,![]()
所以函数![]() 在
在![]() 上有唯一的零点.
上有唯一的零点.
又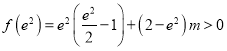
所以函数![]() 在
在![]() 上有唯一的零点.
上有唯一的零点.
综上所述:实数![]() 的取值范围为
的取值范围为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某良种培育基地正在培育一种小麦新品种A.将其与原有的一个优良品种B进行对照试验.两种小麦各种植了25亩,所得亩产数据(单位:千克)如下:
品种A:357,359,367,368,375,388,392,399,400,405,412, 414,415,421,423,423,427,430,430,434,443,445,445,451,454
品种B:363,371,374,383,385,386,391,392,394,394,395, 397,397,400,401,401,403,406,407,410,412,415,416,422,430
(1)作出茎叶图;
(2)通过观察茎叶图,对品种A与B的亩产量及其稳定性进行比较,写出统计结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() 的圆心为
的圆心为![]() ,圆
,圆![]() :
:![]() 的圆心为
的圆心为![]() ,一动圆与圆
,一动圆与圆![]() 内切,与圆
内切,与圆![]() 外切.
外切.
(1)求动圆圆心![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 是直线
是直线![]() 上任意点,直线
上任意点,直线![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,试探求
,试探求![]() ,
,![]() ,
,![]() 的关系,并给出证明.
的关系,并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,抛物线
,抛物线![]() 的焦点
的焦点![]() 恰好是该椭圆的一个顶点.
恰好是该椭圆的一个顶点.
(1)求椭圆![]() 的方程;
的方程;
(2)已知圆![]() 的切线
的切线![]() (直线
(直线![]() 的斜率存在且不为零)与椭圆相交于
的斜率存在且不为零)与椭圆相交于![]() 、
、![]() 两点,那么以
两点,那么以![]() 为直径的圆是否经过定点?如果是,求出定点的坐标;如果不是,请说明理由.
为直径的圆是否经过定点?如果是,求出定点的坐标;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,若曲线
,若曲线![]() 与曲线
与曲线![]() 关于直线
关于直线![]() 对称.
对称.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 的异于极点的交点为
的异于极点的交点为![]() ,与
,与![]() 的异于极点的交点为
的异于极点的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P(x0,y0)在曲线y=x2(x>0)上.已知A(0,-1),![]() ,n∈N*.记直线APn的斜率为kn.
,n∈N*.记直线APn的斜率为kn.
(1)若k1=2,求P1的坐标;
(2)若k1为偶数,求证:kn为偶数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左焦点为
的左焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
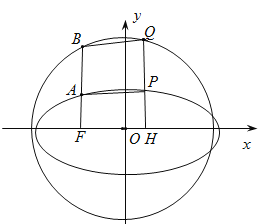
(1)求椭圆![]() 的方程;
的方程;
(2)已知圆![]() ,连接
,连接![]() 并延长交圆
并延长交圆![]() 于点
于点![]() 为椭圆长轴上一点(异于左、右焦点),过点
为椭圆长轴上一点(异于左、右焦点),过点![]() 作椭圆长轴的垂线分别交椭圆
作椭圆长轴的垂线分别交椭圆![]() 和圆
和圆![]() 于点
于点![]() (
(![]() 均在
均在![]() 轴上方).连接
轴上方).连接![]() ,记
,记![]() 的斜率为
的斜率为![]() ,
,![]() 的斜率为
的斜率为![]() .
.
①求![]() 的值;
的值;
②求证:直线![]() 的交点在定直线上.
的交点在定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,双曲线![]() 的右顶点为A,右焦点为F,点B在双曲线的右支上,矩形OFBD与矩形AEGF相似,且矩形OFBD与矩形AEGF的面积之比为2:1,则该双曲线的离心率为
的右顶点为A,右焦点为F,点B在双曲线的右支上,矩形OFBD与矩形AEGF相似,且矩形OFBD与矩形AEGF的面积之比为2:1,则该双曲线的离心率为

A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com