
【题目】以下四个命题中其中真命题个数是( )
①为了了解800名学生的成绩,打算从中抽取一个容量为40的样本,考虑用系统抽样,则分段的间隔k为40;
②线性回归直线![]() 恒过样本点的中心
恒过样本点的中心![]() ;
;
③随机变量ξ服从正态分布N(2,σ2)(σ>0),若在(﹣∞,1)内取值的概率为0.1,则在(2,3)内的概率为0.4;
④若事件![]() 和
和![]() 满足关系
满足关系![]() ,则事件
,则事件![]() 和
和![]() 互斥.
互斥.
A. 0 B. 1 C. 2 D. 3
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC中,PC⊥平面ABC,PC=3,∠ACB= ![]() .D,E分别为线段AB,BC上的点,且CD=DE=
.D,E分别为线段AB,BC上的点,且CD=DE= ![]() ,CE=2EB=2
,CE=2EB=2 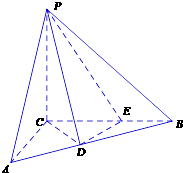
(1)证明:DE⊥平面PCD
(2)求二面角B﹣PD﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A,B,C所对的边分别是a,b,c,B是钝角,且 ![]() a=2bsinA.
a=2bsinA.
(1)求B的大小;
(2)若△ABC的面积为 ![]() ,且b=7,求a+c的值;
,且b=7,求a+c的值;
(3)若b=6,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2000多年前,古希腊大数学家阿波罗尼奥斯((Apollonius)发现:平面截圆锥的截口曲线是圆锥曲线.已知圆锥的高为![]() ,
, ![]() 为地面直径,顶角为
为地面直径,顶角为![]() ,那么不过顶点
,那么不过顶点![]() 的平面;与
的平面;与![]() 夹角
夹角![]() 时,截口曲线为椭圆;与
时,截口曲线为椭圆;与![]() 夹角
夹角![]() 时,截口曲线为抛物线;与
时,截口曲线为抛物线;与![]() 夹角
夹角![]() 时,截口曲线为双曲线.如图,底面内的直线
时,截口曲线为双曲线.如图,底面内的直线![]() ,过
,过![]() 的平面截圆锥得到的曲线为椭圆,其中与
的平面截圆锥得到的曲线为椭圆,其中与![]() 的交点为
的交点为![]() ,可知
,可知![]() 为长轴.那么当
为长轴.那么当![]() 在线段
在线段![]() 上运动时,截口曲线的短轴顶点的轨迹为( )
上运动时,截口曲线的短轴顶点的轨迹为( )
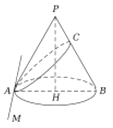
A. 圆的部分 B. 椭圆的部分 C. 双曲线的部分 D. 抛物线的部分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,内角A,B,C的对边分别为a,b,c,且2asinB= ![]() b.
b.
(1)求角A的大小;
(2)若a=6,b+c=8,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上. 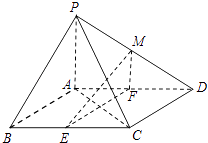
(1)求证:EF⊥平面PAC;
(2)如果直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com