
分析 (1)当a=1时,求出F(x)=x[f(x)-f′(x)],求出函数的导数,然后求解最小值.
(2)通过当a≤0时,推出a≥[-e2x]max,当a>0时,推出a≤[e2x]min,然后求出a的范围.
解答 解:(1)当a=1时,函数$f(x)={e^x}-\frac{a}{e^x}$=${e}^{x}-\frac{1}{{e}^{x}}$.
F(x)=x[f(x)-f′(x)],F(x)=$-\frac{2x}{{e}^{x}}$.
F′(x)=$\frac{2(x-1)}{{e}^{x}}$=0,可得x=1.
由表得:当x=1时,
F(x)最小值为:-$\frac{2}{e}$.┉┉┉(5分)
(2)当a≤0时,f(x)=${e}^{x}-\frac{a}{{e}^{x}}$>0,g(x)=f(x),
若在[0,1]上单调递增,则f′(x)≥0恒成立,即:a≥[-e2x]max,
a≥-1,
∴-1≤a≤0,┉┉┉(8分)
当a>0时,f′(x)=${e}^{x}+\frac{a}{{e}^{x}}$>0,f(x)=${e}^{x}-\frac{a}{{e}^{x}}$在[0,1]上是单调增的
又g(x)=|f(x)|在[0,1]上单调递增,所以f(x)≥0在[0,1]上恒成立.a≤[e2x]min,0<a≤1.
综上:-1≤a≤1┉┉┉(12分)
点评 本题考查函数的导数的应用,函数的极值,最小值,分类讨论思想的应用,考查分析问题解决问题的能力.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | $\frac{π}{2}$ | 2π | $\frac{7π}{2}$ | 5π | $\frac{13π}{2}$ |
| y | 0 | 2 | 0 | -2 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
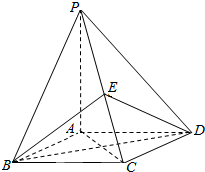 如图4,四边形ABCD为菱形,∠ABC=60°.PA⊥平面ABCD,E为PC中点.
如图4,四边形ABCD为菱形,∠ABC=60°.PA⊥平面ABCD,E为PC中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
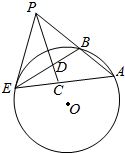 如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线与AE,BE分别交于点C,D.
如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线与AE,BE分别交于点C,D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{3}$ | B. | -4$\sqrt{3}$ | C. | ±4$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)有最小值2 | B. | 函数f(x)有最大值2 | C. | 函数f(x)有最小值3 | D. | 函数f(x)有最大值3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com