
分析 先根据已知条件平方整理得到向量$\overrightarrow a,\overrightarrow b$数量积,再结合基本不等式求出夹角的余弦值的范围,求出结论.
解答 解:因为非零向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a+\overrightarrow b}|=\sqrt{3}|{\overrightarrow a-\overrightarrow b}|$,
所以${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+2\overrightarrow{a}•\overrightarrow{b}=3{\overrightarrow{a}}^{2}-6\overrightarrow{a}•\overrightarrow{b}+3{\overrightarrow{b}}^{2}$,
整理得$\overrightarrow{a}•\overrightarrow{b}=\frac{1}{4}({\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2})$≥$\frac{1}{2}|\overrightarrow{a}||\overrightarrow{b}|$,
所以向量$\overrightarrow a,\overrightarrow b$夹角的余弦值cosθ$≥\frac{1}{2}$,
所以向量$\overrightarrow a,\overrightarrow b$夹角的取值范围为[0,$\frac{π}{3}$];
故答案为:[0,$\frac{π}{3}$].
点评 本题主要考察数量积表示两个向量的夹角以及基本不等式的应用.属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 0或3 | B. | 0或4 | C. | 0或5 | D. | 0或6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{5}{12}$ | C. | $\frac{7}{18}$ | D. | $\frac{13}{36}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
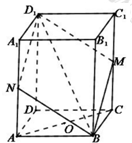 如图,在长方体ABCD-A1B1C1D1中,面BMD1N与棱CC1,AA1分别交于点M,N,且M,N均为中点.
如图,在长方体ABCD-A1B1C1D1中,面BMD1N与棱CC1,AA1分别交于点M,N,且M,N均为中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (1,-2) | C. | (4,3) | D. | (4,-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+6 | 5 | 6 | 7 | 8 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com