
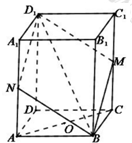
 如图,在长方体ABCD-A1B1C1D1中,面BMD1N与棱CC1,AA1分别交于点M,N,且M,N均为中点.
如图,在长方体ABCD-A1B1C1D1中,面BMD1N与棱CC1,AA1分别交于点M,N,且M,N均为中点.分析 (1)连接MN,证明四边形ACMN为平行四边形,所以AN∥MN,利用线面平行的判定定理证明AC∥面BMD1N;
(2)当点F满足D1F=3BF时,面ACF⊥面BD1E,证明AC⊥OF,MN⊥OF,即可得出结论.
解答 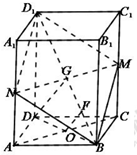 (1)证明:连接MN,因为M,N均为中点,所以$AN=\frac{1}{2}A{A_1},CM=\frac{1}{2}C{C_1}$,
(1)证明:连接MN,因为M,N均为中点,所以$AN=\frac{1}{2}A{A_1},CM=\frac{1}{2}C{C_1}$,
又因为AA1∥CC1,且AA1=CC1,所以AN∥CM,且AN=CM,
所以四边形ACMN为平行四边形,所以AN∥MN,
又因为MN?面BMD1N,AC?面BMD1N,所以AC∥面BMD1N;
(2)解:当点F满足D1F=3BF时,面ACF⊥面BD1E,证明如下:
连接BD交AC于O,则BD经过点O,取BD1中点G,连接OF,DG,
则OF为三角形BDG边DG上的中位线,所以OF∥DG,
因为$B{D_1}=2\sqrt{2}=D{D_1}$,且G为BD1的中点,所以BD1⊥DG,所以BD1⊥OF,
因为底面ABCD为正方形,所以AC⊥BD,又DD1⊥底面ABCD,所以AC⊥DD1,
又BD∩DD1=D,所以AC⊥面BDD1,又OF?面BDD1,所以AC⊥OF,
由第(1)问知AC∥MN,所以MN⊥OF,
又MN,BD1是平面四边形BMD1N的对角线,所以它们必相交,所以OF⊥面BMD1N.
点评 本题主要考查立体几何中线面平行,线面垂直的证明,做题时综合考查了学生的识图能力,空间想象的能力以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1} | B. | {1} | C. | {3} | D. | {-1,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,3) | B. | {4,-3} | C. | {(4,3)} | D. | {(4,-3)} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com