
分析 (1)求出函数的对称轴,列出不等式求解即可.
(2)f(2)的表达式,结合(1)a的范围,求解f(2)d的取值范围即可.
解答 解:(1)∵对称轴$x=\frac{a-1}{2}$,二次函数f(x)=x2-(a-1)x+5在区间($\frac{1}{2}$,1)上是增函数,
联系图象,满足题意,
只需$\frac{a-1}{2}≤\frac{1}{2}$,
∴a≤2; …(6分)
(2)∵f(2)=22-2(a-1)+5=-2a+11,
又∵a≤2,
∴-2a≥-4,
∴f(2)=-2a+11≥-4+11=7,
∴f(2)∈[7,+∞).…(12分)
点评 本题考查二次函数的简单性质的应用,考查转化思想以及计算能力.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
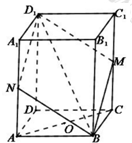 如图,在长方体ABCD-A1B1C1D1中,面BMD1N与棱CC1,AA1分别交于点M,N,且M,N均为中点.
如图,在长方体ABCD-A1B1C1D1中,面BMD1N与棱CC1,AA1分别交于点M,N,且M,N均为中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+6 | 5 | 6 | 7 | 8 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com