
某一几何体的三视图如图所示.按照给出的尺寸(单位:cm),(1)请写出该几何体是由哪些简单几何体组合而成的;(2)求出这个几何体的体积.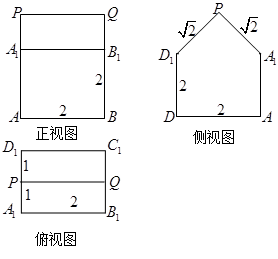
 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:解答题
如图,在三棱柱ABC﹣A1B1C1中,AA1⊥底面ABC,且△ABC为正三角形,AA1=AB=6,D为AC的中点.
(1)求证:直线AB1∥平面BC1D;
(2)求证:平面BC1D⊥平面ACC1A;
(3)求三棱锥C﹣BC1D的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知正△ABC的边长为 , CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
, CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
(1)试判断折叠后直线AB与平面DEF的位置关系,并说明理由;
(2)若棱锥E-DFC的体积为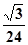 ,求
,求 的值;
的值;
(3)在线段AC上是否存在一点P,使BP⊥DF?如果存在,求出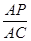 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.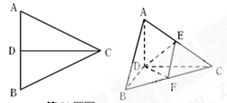
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
设直线 与球O有且仅有一公共点P,从直线
与球O有且仅有一公共点P,从直线 出发的两个半平面截球O的两个截面圆O1和圆O2的半径1和2,若这两个半平面
出发的两个半平面截球O的两个截面圆O1和圆O2的半径1和2,若这两个半平面 ,
, 所成二面角为1200,则球O的表面积为 。
所成二面角为1200,则球O的表面积为 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com