
分析 (1)求出方案甲、乙的平均价格,作差,即可进行比较;
(2)求出方案丙、定的价格,作差,即可进行比较.
解答 解:(1)方案甲平均价格为$\frac{ma+mb}{2m}$=$\frac{a+b}{2}$,方案乙平均价格为$\frac{2n}{\frac{n}{a}+\frac{n}{b}}$=$\frac{2ab}{a+b}$,
∵$\frac{a+b}{2}$-$\frac{2ab}{a+b}$=$\frac{(a-b)^{2}}{2(a+b)}$>0,
∴方案乙平均价格较小;
(2)方案丙:第一次提价p,第二次提价q,则价格为100(1+p)(1+q),
方案丁:第一次提价$\frac{p+q}{2}$,第二次提价$\frac{p+q}{2}$,则价格为$100(1+\frac{p+q}{2})^{2}$,
∵100(1+p)(1+q)-$100(1+\frac{p+q}{2})^{2}$=-100$(\frac{p-q}{2})^{2}$>0,
∴按照方案丁提价后的价格较高.
点评 本题考查利用数学知识解决实际问题,考查作差方法的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$) | B. | (0,1) | C. | ($\frac{1}{2}$,1) | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $-\frac{{\sqrt{2}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
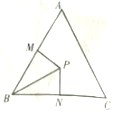 如图,△ABC三个内角A,B,C所对的边分别为a,b,c,已知C=$\frac{π}{3}$,$\frac{a}{b}$=$\frac{cosB}{cosA}$,在△ABC内取一点P,使得PB=3,过点P分别作直线BA,BC的垂线PM,PN,垂足分别是M,N,则|PM|+|PN|的最大值为3.
如图,△ABC三个内角A,B,C所对的边分别为a,b,c,已知C=$\frac{π}{3}$,$\frac{a}{b}$=$\frac{cosB}{cosA}$,在△ABC内取一点P,使得PB=3,过点P分别作直线BA,BC的垂线PM,PN,垂足分别是M,N,则|PM|+|PN|的最大值为3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com