
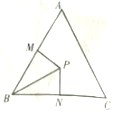
 如图,△ABC三个内角A,B,C所对的边分别为a,b,c,已知C=$\frac{π}{3}$,$\frac{a}{b}$=$\frac{cosB}{cosA}$,在△ABC内取一点P,使得PB=3,过点P分别作直线BA,BC的垂线PM,PN,垂足分别是M,N,则|PM|+|PN|的最大值为3.
如图,△ABC三个内角A,B,C所对的边分别为a,b,c,已知C=$\frac{π}{3}$,$\frac{a}{b}$=$\frac{cosB}{cosA}$,在△ABC内取一点P,使得PB=3,过点P分别作直线BA,BC的垂线PM,PN,垂足分别是M,N,则|PM|+|PN|的最大值为3. 分析 由acosA=bcosB及正弦定理可得:sinAcosA=sinBcosB,即sin2A=sin2B,又A∈(0,π),B∈(0,π),可得A=B或A+B=$\frac{π}{2}$. 由于C=$\frac{π}{3}$,即可得出B,设∠PBM=α,得PM=3sinα;PN=3sin($\frac{π}{3}$-α),α∈(0,$\frac{π}{3}$).于是PM+PN=3sin(α+$\frac{π}{3}$).由于α∈(0,$\frac{π}{3}$),可得sin(α+$\frac{π}{3}$)∈($\frac{\sqrt{3}}{2}$,1],即可得出.
解答 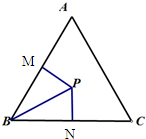 解:由$\frac{a}{b}$=$\frac{cosB}{cosA}$,及正弦定理可得:sinAcosA=sinBcosB,
解:由$\frac{a}{b}$=$\frac{cosB}{cosA}$,及正弦定理可得:sinAcosA=sinBcosB,
即sin2A=sin2B,又A∈(0,π),B∈(0,π),
∴有A=B或A+B=$\frac{π}{2}$.
又∵C=$\frac{π}{3}$,得A+B=$\frac{2π}{3}$,与A+B=$\frac{π}{2}$矛盾,
∴A=B,因此B=$\frac{π}{3}$.
设∠PBM=α,可得:
在Rt△PMB中,PM=PB•sin∠PBM=3sinα;
在Rt△PNB中,PN=PB•sin∠PBN=PB•sin($\frac{π}{3}$-∠PBA)=3sin($\frac{π}{3}$-α),α∈(0,$\frac{π}{3}$).
∴PM+PN=3sinα+3sin($\frac{π}{3}$-α)=3sin(α+$\frac{π}{3}$).
∵α∈(0,$\frac{π}{3}$),∴α+$\frac{π}{3}$∈($\frac{π}{3}$,$\frac{2π}{3}$),从而有sin(α+$\frac{π}{3}$)∈($\frac{\sqrt{3}}{2}$,1],
即3sin(α+$\frac{π}{3}$)∈($\frac{3\sqrt{3}}{2}$,3].
于是,当α+$\frac{π}{3}$=$\frac{π}{2}$,即α=$\frac{π}{6}$时,PM+PN取得最大值3.
故答案为:3.
点评 本题查克拉正弦定理、倍角公式、和差公式、三角函数的单调性,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 吴敬《九章算法比类大全》中描述:遥望巍巍塔七层,红光点点倍加增;共灯三百八十一,试问塔顶几盏灯?类比等比数列的知识可得灯塔的灯数为( )
吴敬《九章算法比类大全》中描述:遥望巍巍塔七层,红光点点倍加增;共灯三百八十一,试问塔顶几盏灯?类比等比数列的知识可得灯塔的灯数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-15,$\frac{1}{5}$] | B. | [-$\frac{5}{3}$,$\frac{9}{5}$] | C. | [-$\frac{5}{3}$,$\frac{1}{5}$] | D. | [-15,$\frac{9}{5}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$] | B. | [$\frac{1}{2}$,$\frac{2}{3}$) | C. | ($\frac{2}{3}$,1] | D. | [1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com