练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．吴敬《九章算法比类大全》中描述：遥望巍巍塔七层，红光点点倍加增；共灯三百八十一，试问塔顶几盏灯？类比等比数列的知识可得灯塔的灯数为（　　）
    A．1B．2C．3D．4

    分析 设每层的灯数组成等比数列{an}，S7=381，公比q=2．利用等比数列的前n项和公式即可得出．

    解答 解：设每层的灯数组成等比数列{an}，S7=381，公比q=2．
    ∴$\frac{{a}_{1}（{2}^{7}-1）}{2-1}$=381，
    解得a1=3．
    故选：C．

    点评 本题考查了等比数列的等比数列的前n项和公式，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    12．已知函数f（x）=$\left\{\begin{array}{l}{x^2}+4x，\;\;\;\;\;\;\;x≥0\\ 4x-{x^2}，\;\;\;\;\;\;\;x＜0\end{array}$，则不等式$f（{\sqrt{x}}）＞f（{2x}）$的解集是{x|0＜x＜$\frac{1}{4}$}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知x，y满足$\left\{\begin{array}{l}{x≥1}\\{x+y≤4}\\{x-y-3≤0}\end{array}\right.$则目标函数z=2x+y的最大值为7.5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．设函数f（x）=x2-2tx+2，其中 t∈R．
    （1）若t=1，求函数f（x）在区间[0，4]上的取值范围；
    （2）若t=1，且对任意的x∈[a，a+2]，都有f（x）＜5，求实数a的取值范围；
    （3）若对任意的x1，x2∈[0，4]，都有f（x1）-f（x2）≤8，求t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率$e=\frac{{\sqrt{3}}}{2}，A、B$，分别是椭圆的左、右顶点，点P是椭圆上的一点，直线PA、PB的倾斜角分别为α、β满足tanα+tanβ=1，则直线PA的斜率为$\frac{{1±\sqrt{2}}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

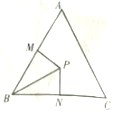    7．如图，△ABC三个内角A，B，C所对的边分别为a，b，c，已知C=$\frac{π}{3}$，$\frac{a}{b}$=$\frac{cosB}{cosA}$，在△ABC内取一点P，使得PB=3，过点P分别作直线BA，BC的垂线PM，PN，垂足分别是M，N，则|PM|+|PN|的最大值为3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．集合A={x|$\frac{1}{2}$＜2x≤4}，则 A∩Z={0，1，2}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．下列命题：
    ①偶函数的图象一定与y轴相交；  
     ②定义在R上的奇函数f（x）必满足f（0）=0；
    ③f（x）=（2x+1）2-2（2x-1）既不是奇函数又不是偶函数；
    ④f（x）=$\frac{1}{x}$在（-∞，0）∪（0，+∞）上是减函数．其中真命题的序号是②．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知$\overrightarrow{a}$=（x，0），$\overrightarrow{b}$=（1，y），且（$\overrightarrow{a}$+$\sqrt{3}$$\overrightarrow{b}$）⊥（$\overrightarrow{a}$-$\sqrt{3}$$\overrightarrow{b}$）．
    （1）求点P（x，y）的轨迹C的方程；
    （2）若直线y=kx+m（k≠0）与曲线C交于A，B两点，D（0，-1），且|AD|=|DB|，试求实数m的取值范围．

    查看答案和解析>>

    同步练习册答案