
分析 求出抛物线y2=2px(p>0)的准线方程,利用抛物线y2=2px(p>0)的准线与圆(x-3)2+y2=225相切,可得p,利用双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线方程是y=$\sqrt{3}$x,它的一个焦点是该抛物线的焦点,$\frac{b}{a}$=$\sqrt{3}$,a2+b2=144,即可求出双曲线实轴长.
解答 解:抛物线y2=2px(p>0)的准线方程为x=-$\frac{p}{2}$,
∵抛物线y2=2px(p>0)的准线与圆(x-3)2+y2=225相切,
∴3+$\frac{p}{2}$=15,∴p=24,
∵双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线方程是y=$\sqrt{3}$x,它的一个焦点是该抛物线的焦点,
∴$\frac{b}{a}$=$\sqrt{3}$,a2+b2=144,
∴a=6,b=6$\sqrt{3}$,
∴2a=12,
∴双曲线实轴长为12.
故答案为:12.
点评 本题考查双曲线实轴长,考查双曲线、抛物线的性质,属于中档题.


科目:高中数学 来源: 题型:解答题
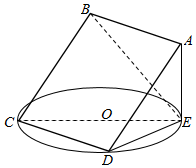 如图所示,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C,D的点,AE=3,圆O的直径为9.
如图所示,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C,D的点,AE=3,圆O的直径为9.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “若x≠a且x≠b,则x2-(a+b)x+ab≠0”的否命题是“若x=a或x=b,则x2-(a+b)x+ab=0” | |
| B. | 若p∧q为假命题,则p,q均为假命题 | |
| C. | 命题“?x0∈(0,+∞)lnx0=x0-1”的否定是“?x∈(0,+∞),lnx≠x-1 | |
| D. | “x>2”是“$\frac{1}{x}$<$\frac{1}{2}$”的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 7 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-cos1 | B. | 1-cos2 | C. | cos2-1 | D. | cos1-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com