
(1)如果CD⊥AB,求证:EN=MN.
(2)如果弦CD交AB于点F,且CD=AB,求证:CE2=EF·ED.
(3)如果弦CD、AB的延长线交于点F,且CD=AB,那么(2)的结论是否仍成立?若成立,请证明;若不成立,请说明理由.
图
(1)证明:连结BM,∵CD⊥AB,
∴∠BCE+∠ABC=90°.
∵AM是直径,∴∠MBN+∠ABC=90°.
∴∠BCE=∠MBN.
又∵ON⊥BC,∴BN=CN,∠BNM=∠CNE.
∴△BNM≌△CNE.
∴EN=MN.
(2)证明:连结BD、BE、AC.
∵CD=AB![]()
![]()
![]() ∠ACD=∠D.
∠ACD=∠D.

![]() △ABE≌△ACE
△ABE≌△ACE![]() ∠ACD=∠ABE.
∠ACD=∠ABE.
![]()
![]() △BEF∽△DEB
△BEF∽△DEB![]()
![]() =
=

(3)如图

图
证明:∵AM⊥BC,
∴BE=CE,AB=AC.
∴∠1=∠2,∠3=∠4.
∵AB=CD,
∴∠4=∠DBC.
∴∠3=∠DBC=∠2+∠5.
又∵∠3=∠F+∠1,∴∠F=∠5.
∵∠BED=∠FEB,∴△BDE∽△FBE.
∴![]() .
.
∴BE2=EF·ED.∴CE2=EF·ED.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
A.90° B.60° C.45° D.30°

图2-1-17
查看答案和解析>>
科目:高中数学 来源: 题型:
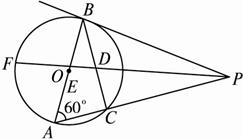
图2-4-17
(1)求证:PA·BD=PB·AE;
(2)证明⊙O的直径长为常数;
(3)求tan∠FPA的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
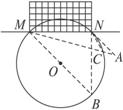
图2-1-17
查看答案和解析>>
科目:高中数学 来源: 题型:

图2-5-17
查看答案和解析>>
科目:高中数学 来源: 题型:
如图2-1-17,空间四边形SABC中,各边及对角线长都相等,若E、F分别为SC、AB的中点,那么异面直线EF与SA所成的角等于( )
A.90° B.60° C.45° D.30°
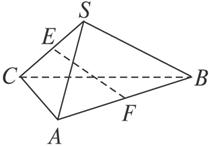
图2-1-17
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com