
���� ��1���������ַ��̵Ļ���������������ֱ��l����ͨ���̺�Բ��C ��ֱ�����ꣻ
��2��ԲC�İ뾶r=1�����Բ�ĵ�ֱ�ߵľ��룬���������߳�����Сֵ��
��� �⣺��1��ֱ��l����ͨ����Ϊ$y=x+4\sqrt{2}$��
��$��=2cos����+\frac{��}{4}��$��${��^2}=\sqrt{2}��cos��-\sqrt{2}��sin��$
��ԲC����ͨ����Ϊ${x^2}+{y^2}=\sqrt{2}x-\sqrt{2}y$����${x^2}+{y^2}-\sqrt{2}x+\sqrt{2}y=0$
Բ��C��ֱ������Ϊ $��\frac{{\sqrt{2}}}{2}��-\frac{{\sqrt{2}}}{2}��$��
��2��ԲC�İ뾶r=1��Բ�ĵ�ֱ�ߵľ���$d=\frac{{|\frac{{\sqrt{2}}}{2}+\frac{{\sqrt{2}}}{2}+4\sqrt{2}|}}{{\sqrt{2}}}=5$
�����߳�����СֵΪ$\sqrt{{d^2}-{r^2}}=\sqrt{{5^2}-{1^2}}=\sqrt{6��4}=2\sqrt{6}$��
���� ���⿼�����ַ��̵Ļ���������ֱ����Բ��λ�ù�ϵ������ѧ���ļ��������������е��⣮


 ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
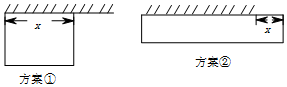 �Ϻ��и��˸���ѧ���ڸ�����������2015��9����ʽ��ʼ������ҪΧ��һ�������900ƽ���ľ��εس��ص�Χǽ����һ�泤��Ϊ20�ľ�ǽ��ͼ��б�ܲ������мס�������ά�����þ�ǽ������
�Ϻ��и��˸���ѧ���ڸ�����������2015��9����ʽ��ʼ������ҪΧ��һ�������900ƽ���ľ��εس��ص�Χǽ����һ�泤��Ϊ20�ľ�ǽ��ͼ��б�ܲ������мס�������ά�����þ�ǽ�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | sinx | B�� | -sinx | C�� | cosx | D�� | -cosx |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com