
 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题
已知二次函数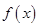 的顶点坐标为
的顶点坐标为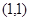 ,且
,且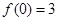 ,
,
(1)求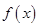 的解析式,
的解析式,
(2)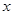 ∈
∈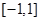 ,
,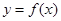 的图象恒在
的图象恒在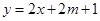 的图象上方,
的图象上方,
试确定实数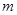 的取值范围,
的取值范围,
(3)若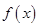 在区间
在区间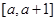 上单调,求实数
上单调,求实数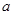 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
首届世界低碳经济大会在南昌召开,本届大会以“节能减排,绿色生态”为主题.某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本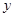 (元)与月处理量
(元)与月处理量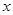 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: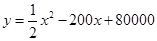 ,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(Ⅰ)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(Ⅱ)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
统计表明,某种型号的汽车在匀速行驶中每小时的耗油量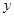 (升)关于行驶速度
(升)关于行驶速度 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: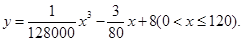 已知甲、乙两地相距100千米。
已知甲、乙两地相距100千米。
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
汽车和自行车分别从 地和
地和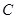 地同时开出,如下图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知
地同时开出,如下图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知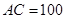 米.(汽车开到
米.(汽车开到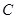 地即停止)
地即停止)
(Ⅰ)经过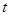 秒后,汽车到达
秒后,汽车到达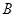 处,自行车到达
处,自行车到达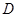 处,设
处,设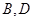 间距离为
间距离为 ,试写出
,试写出 关于
关于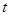 的函数关系式,并求其定义域.
的函数关系式,并求其定义域.
(Ⅱ)经过多少时间后,汽车和自行车之间的距离最短?最短距离是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com